short summary!
確率の問題では(問題の設定に関わらず)物と組を区別するのが得策
はじめに
確率の問題を解いていると「同様に確からしい」という言葉に出会うでしょう.しかもかなり序盤のはずです.
にも関わらず,意外と理解出来ている人が少なく,混乱しがちなところ.
この記事を読めば「同様に確からしい」について完璧に理解できるはずです.
頑張っていきましょう!
もくじ
「同様に確からしい」とは
確率の問題において,事象$E$の起こる確率$P(E)$は,全事象の場合の数$n(U)$と事象$E$の起こる場合の数$n(E)$を用いて
$\displaystyle P(E)=\frac{n(E)}{n(U)}$
と表されます.上の式において,全事象$n(U)$は「同様に確からしく」なくてはなりません.
「同様に確からしい(be equally likely)」とは確率の問題を解く上での原則です.くだけた説明をすると,「ひとつひとつがどれも同じ確率で起こる」とでも表現できます.
高校数学では「根元事象は同様に確からしい」というルールのもと,問題を解いて行くこととなります.(「根元事象」とは,起こりうる最小単位の出来事のことです.)
今回覚えておいてほしいことはひとつで
物・組を全て区別した場合,同様に確からしくなる(=正しく確率の問題が解ける)
ということ.
以下のような問題を考えてみましょう.
赤球が3個と白球が2個入った箱からひとつ取り出したとき,それが赤である確率を求めよ.
【解1(誤答)】
取り出す色は赤か白かの2通りなので,確率は$\displaystyle \frac12$
【解2(正答)】
全ての球を区別すると,取り出し方の総数は5通り.
一方,赤球を取り出す場合の数は3通りなので,求める確率は$\displaystyle \frac35$
解1が誤答であるのはなんとなく分かるでしょう.これがもし場合の数の問題で,
「赤球が3個と白球が2個入った箱からひとつ取り出したとき,何通りの取り出し方があるか.」
と問われれば,当然答えは赤と白の2通りなんです.解1が間違いである理由は,
「取り出す色は赤か白かの2通り」
の部分が同様に確からしくない
(=赤の取り出される確率と白の取り出される確率が異なる)
からです.
多くの問題では,何を「同様に確からしい」と捉えるかは明白なのですが,以下の問題のように,それが曖昧で答えに迷ってしまうこともあります.
例題
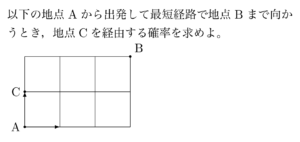
【解1】
AからBまで向かうのは→3つと↑2つの順列で
$\displaystyle \frac{5!}{3!\cdot2!}=10$(通り)
このうちA→C→Bと向かうのは
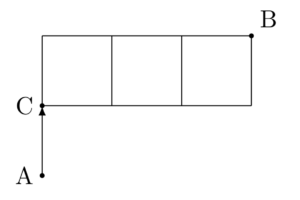
同様に考えて4通りなので,求める確率は
$\displaystyle \frac4{10}=\frac25$
【解2】
AからBまで向かう際に,↑と→を同確率で進んでいくと考えて,Cを通るときははじめに↑を選ぶ確率と等しく,求める確率は
$\displaystyle \frac12$
さて,どちらが正しい答えでしょう.結論からいうと,「どちらも正しい」が答えです.
解1では,「AからBへ向かう道順6通りを同様に確からしく選ぶ」という考えかたである一方で,
解2では,「↑と→を同様に確からしく選ぶ(行き止まりでは一方しか選べない)」という考え方のもとこの問題を解いています.
このように,何を同様に確からしいと捉えるかによって確率は変わってくるのですね.基本的に入試問題などではこの辺りを明確にしてくれていることが多いです.
まとめ
「同様に確からしい」とは「1つ1つの場合の数が同じ確率で起こる」という意味で,確率の問題を解くためのルール
「物・組を全て区別した場合の数」を考えることで,正しく確率を求めることが出来る

