もくじ
解答解説
問題
座標平面において,
(1) 平行四辺形OABCの内部(辺,頂点は含めない)に格子点はいくつあるか.
(2) (1)の格子点全体を
格子点と整数がテーマです.
格子点の数え方は積分とほとんど同じです.
ある軸(
(1)はそこまで悩まずに答えが出ると思いますが,(2)が問題です.
まず,三角形の面積をどう表すかは大丈夫でしょうか.
本サイトでは7通りの表現を紹介していますが,平面座標で,整数という条件を使わなければならないことを考えると,
と表せたのではないでしょうか.
次に,先にも書いたように「整数」について
「
に反応できたでしょうか.
これは「互いに素」ですよね.扱い方を確認しておきましょう.
-

-
「互いに素」の性質と使い方まとめ
short summary! 「互いに素」の2つの定義 ・最大公約数が
続きを見る
整数条件の中でも「素数」「互いに素」と言った条件はやっぱり超強力です.無視することのないように.
今回は,
→
という有名事項を思い出さなければなりません.証明はぜひ覚えておいて欲しいのでまとめに記しておきます.
ここは経験が必要でなかなか考えづらかったかもしれませんね.最小値
解答
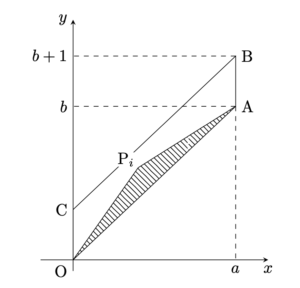
平行四辺形OABCの内部は,不等式
によって表される.
に対して,
よって,
(2)
格子点を
と表せる.
②より,
である.ここで,異なる正の整数
とすると,移項して,
が成立する.
よって,
④と合わせて,
本問で覚えておきたい論証
・互いに素に関する性質
【証明】
よって
↓この性質から分かること
つまり,

