「互いに素」の性質と使い方まとめ

はじめに

「互いに素」という条件は有理数や最大公約数などの問題で登場します．

素数とともに強い条件ですので，「互いに素の利用」と「互いに素の証明」の両方を得意にしていきましょう．

「互いに素」の定義

まずは以下の２つを頭に叩き込みましょう．互いに素数，では決してないので気をつけてください．

初めて習うときは「肯定」のことが多いのではないでしょうか．ですが公約数は素因数によって決定されるものです．

本質的には「否定」の方が理解すべきところでしょう．

素因数が出てくるので，やはり互いに素は強力な条件なのですね．この2つの定義を軸に，以下の内容を理解していきましょう．

以下では$a,\,b$は互いに素な2整数とします．

「互いに素」の利用

まずは①からです．

例えば，

$a=(x+2y)g$
$b=(3x+5y)g$

という式を見てください．$g$は$a,\,b$にとってどういう数でしょうか．

右辺が因数分解されているわけですから$g$は約数ですね．

2数の公約数は．最大公約数の約数です．互いに素な2数の最大公約数は1ですから，$g=1$と決まるのですね．

少し応用ですが．

$2a=(x+2y)g$
$3b=(3x+5y)g$

という式ならどうでしょう．$g$は$2a,\,3b$の公約数ですね．

$a,\,b$には共通する素因数がないので，$g$が持ちうる素因数は$2,\,3$を一つずつです．

つまり，「$g$は6の約数」ということがわかります．

一般化すると「$Xa,\,Yb$の公約数は$X,\,Y$の最小公倍数の約数」と言えるのですが，少し難しいので問題演習でまたお話しします．

②も非常に大事な使い方です．

$a\cdot p=q\cdot b$

この式から

$b$は$a$の素因数を持たない→$a$の素因数を$q$が全て担う
$a$は$b$の素因数を持たない→$b$の素因数を$p$が全て担う

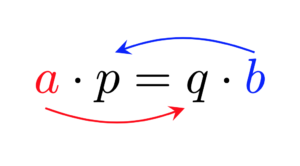
である，つまり

$q$は$a$の倍数→$a$は$q$の約数
$p$は$b$の倍数→$b$は$p$の約数

が成立しています．$q=ak,\,p=bk$と書けるのですね．

高次方程式を解く際，因数定理を利用しますが，解を予想する際に最高次と定数項に注目しますね．

この根拠(click!)が上で述べたことに関係しています．

「互いに素」の証明

互いに素であることの証明は，基本的に定義そのものです．

強調したいのは②の方です．「共通素因数を持たない」ことを示すには，背理法で二重否定の形にして扱うべきでしょう．

素数を置くことで，強力な性質（素数の性質click!）を使うことができます．①よりも②の方が有用です．

まとめ