もくじ
解答解説
問題
双曲線$x^2-y^2=1$上の$1$点$\mathrm{P}(x_0,\,y_0)$から円$x^2+y^2=1$に引いた$2$本の接線の両接点を通る直線を$l$とする．ただし，$y_0\neq0$とする．
(1) 直線$l$は，方程式$x_0x+y_0y=0$で与えられることを示せ．
(2) 直線$l$は，双曲線に接することを証明せよ．
円外の一点から円に接線を引くと，以下のような図になります．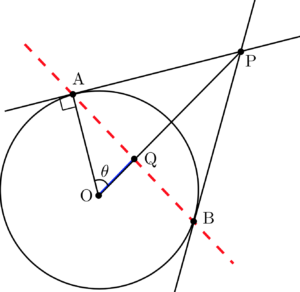
①二本引くことができ，$PA=PB$が成立する
②POは角APBを二等分する
といった性質がありますが，際立っているのが赤線で示した直線です．二つの接点を結んだ直線で，「極線」と呼ばれています．
今回の問題のように，円外の一点から極線の導出をする流れは決まっていて，自力で発想することが難しいどころか，解答を見ても？？？となってしまう人も多いでしょう．以下で解説します．
１．接点A,Bを置いて接線の式を立てる
２．『１で求めた接線が共にPを通る＝代入して成立する』式を立てる
３．２で求めた式を読み替える：最難関
大まかな流れはこんな感じです．
１において理解しておいて欲しいことは，円の接線を考える上で，接点から求めるということです．
「Pを通る直線が円に接する」と考えるのではありません．
そもそも，接線を考える上で
①接点をおく→傾きを求める（微分など）
②接線をおく→重解条件を考える
という２つの方針があります．今回は２接点を通る直線を求めたいのですから，接点をおいてあげましょう．
＜解答（１．まで）＞
$2$接点を$\mathrm{A}(x_1,\,y_1),\,\mathrm{B}(x_2,\,y_2)$とすると，$2$本の接線は，
\begin{align*}
\mathrm{PA}:\,&x_1x+y_1y=1\\
\mathrm{PB}:\,&x_2x+y_2y=1
\end{align*}
と表される．
２．のPを通るので代入するくだりは特に問題ないでしょう．
＜解答（２．まで）＞
点Pはこの直線上であるので，代入して，
\begin{align*}
&x_0x_1+y_0y_1=1\\
&x_0x_2+y_0y_2=1
\end{align*}
が成立している．
次が大問題です．上で得られた式を読み替えます．
何を「読み替える」のか，それは「変数と定数」です．
先ほどまでは接点A,Bが定点で，接線の変数$x,\,y$にPの座標を代入したのですね．
\begin{align*}
&x_0x_1+y_0y_1=1\\
&x_0x_2+y_0y_2=1
\end{align*}
得られたこの式に対して，さっきまでの定数$x_1,\,x_2,\,y_1,\,y_2$を変数$x,\,y$に，さっきまでの変数$x_0,\,y_0$を定数として読み替えると
\[x_0x+y_0y=1\]
という直線が$(x,\,y)=(x_1,\,y_1),\,(x_2,\,y_2)$を満たす，つまりこれはAとBを通るということに他ならないでしょう．
さらに，この段階では『AとBを通る直線をあくまで１つ見つけただけ』です．十分性しか満たしていないので，答案では『他にはない』ことに言及しておきましょう．
式としては円外の一点に対して円の接線公式を使った形になっています．面白くありませんか？
(2)の接することの証明に関してはいくらでもやりようがありますが，今回は式の形に注目して上手に処理をしました．
接点が見えている場合はこういった扱い方もありでしょう．
解答
$2$接点を$\mathrm{A}(x_1,\,y_1),\,\mathrm{B}(x_2,\,y_2)$とすると，$2$本の接線は，
\begin{align*}
\mathrm{PA}:\,&x_1x+y_1y=1\\
\mathrm{PB}:\,&x_2x+y_2y=1
\end{align*}
と表される．点Pはこの直線上であるので，代入して，
\begin{align*}
&x_0x_1+y_0y_1=1\\
&x_0x_2+y_0y_2=1
\end{align*}
が成立している．ここで，$x_0x+y_0y=1$について考えると，上式より$(x,\,y)=(x_1,\,y_1),\,(x_2,\,y_2)$について成立することが分かっているので，この直線は点A,Bを通る．異なる２点を通る直線は唯一つに定まるので，$x_0x+y_0y=1$が$l$の式である．
(2)
点$\mathrm{P}(x_0,\,y_0)$は双曲線$x^2-y^2=1$上であるので，点$\mathrm{P'}(x_0,\,-y_0)$も同じ双曲線上にある．$\mathrm{P'}$における双曲線の接線は
\begin{align*}
&x_0x-(-y_0)y=1\\
\Leftrightarrow\,&x_0x+y_0y=1
\end{align*}
であるので，これは$l$に等しく，題意は示された．