もくじ
解答解説
問題
定数$c$は$-1<c<1$を満たすとする.すべての実数$x$に対して,関係式
\[f(x)+f(cx)=x^2\]
を満たす連続関数$f(x)$を求めよ.
早稲田大学教育学部の問題で,小問集合の(4)ではあるのですが難易度は非常に高いです.
連続性のみが与えられていますが,足して二次関数になるのだから$f(x)$も流石に二次関数になるだろうと予想はできます.
答えだけの問題ですから,適当に$f(x)=Ax^2$と置いて代入してみれば,$A=\dfrac{1}{c^2+1}$と求まってしまいます.入試本番ではこれでいいでしょう.
さて,関数方程式は任意の$x$で成り立つ等式,つまり恒等式です.
「任意の値で成立する」と言う条件が与えられれば,考えることは以下の3つ.
- 数値代入
- (整式なら)係数比較
- (微分可能なら)両辺を微分する
この中で最も大事なのは①数値代入です.(上記の詳しい話はいつか記事にします.)
②③には条件が付きますね.今回のように整式かも微分可能かどうかもわからない場合は使うことができません.
とにかく何らかの値を代入して,関数の具体的なイメージを掴むことが大切になります.
今回はまず$x=0$が候補になるでしょう.邪魔な$c$が消えてくれるからですね.
おそらく多くの人がここより先に進めなかったのではないでしょうか.他に何を代入してもうまくいく未来が見えなかったと思います.
$x=1$や$x=2$を代入したところで,やはり$c$が邪魔なのです.
そこで,\[f(x)+f(cx)=x^2\]という式から$f(cx)$を消去することを目的として,$x$に$cx$を代入した\[f(cx)+f(c^2x)=c^2x^2\]という式を考えてみましょう.
両辺を引くことにより\[f(x)-f(c^2x)=x^2-c^2x^2\]が得られました.
ここで,今まで使っていなかった条件$-1<c<1$に着目できるでしょうか.
\[f(x)+f(cx)=x^2\]と比べて\[f(x)-f(c^2x)=x^2-c^2x^2\]は,$c^2$になった分$0$に近づいたと言えます.
つまり,これを繰り返していけば,$0$に収束することが予想されます.これを解答に起こしたのが以下です.
非常に難解ですが,任意の値で成立する問題に関して,無限大への極限を考えること(無限大への数値代入)と似ていますね.
解答
$x=0$を代入すると$f(0)=0$
1) $c=0$のとき
$f(x)+f(0)=x^2$より$f(x)=x^2$
2) $-1<c<0,\,0<c<1$のとき
与式の$x$に$cx,\,c^2x,\,\cdots,\,c^{n-1}x$を代入すると
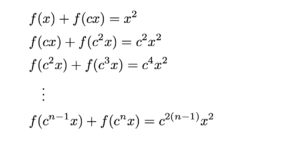
が得られる.
上式において,奇数番目の式を足し,偶数番目の式を引いていくことにより,
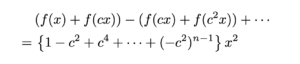
であるので
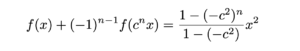
$f(x)$は連続であるため,この両辺に対して$n\to\infty$の極限を考える.$f(0)=0$と$0<c^2<1$であるため,
\[f(x)=\frac{1}{1+c^2}x^2\]
を得る.
以上1)2)より,
\[f(x)=\frac{1}{1+c^2}x^2\]

