もくじ
解答解説
問題
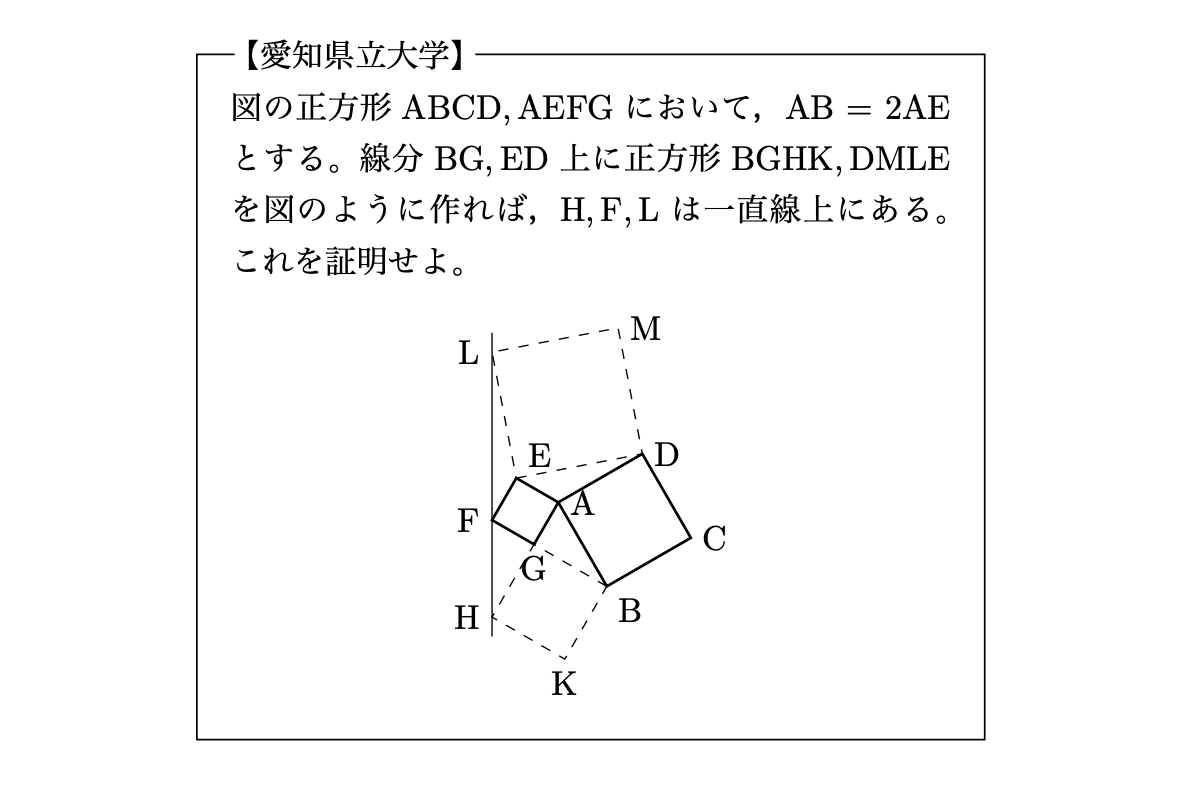
図の正方形ABCD, AEFGにおいて，$\mathrm{AB}=2\mathrm{AE}$とする。線分BG, ED上に正方形BGHK, DMLEを図のように作れば，H, F, Lは一直線上にある。これを証明せよ。
３点以上が同一直線上にあるのは特別な状況．なぜなら，直線は異なる２点で決定するからです．
では，「ABCが同一直線上」をどのように示せば良いのでしょうか．大まかに以下の２通りと考えてもらえればいいと思います．
- 「直線の一致」と考える
直線AB＝直線AC：ABとACが平行
直線AB上にCが存在する，など - 幾何から考える
メネラウスの定理，角ABCが180度，など
基本は，赤で示した通り①のABとACが平行と考えてもらえればいいでしょう．これが一番扱いやすいです．
（明らかな幾何の問題で誘導がついていると，②で考えることもあり得ます）
さて，今回の問題は正方形がたくさん出てきます．
一見すると幾何かな？という気がするのですが，$\mathrm{AB}=2\mathrm{AE}$の条件を使うことを考えると，なかなか幾何では扱いづらかったと思います．
というわけで平行条件を考えるのですが，座標を置くには自由度が高すぎるのが問題になります．
そこで，複素数平面の利用を思いつけたかどうか．
「正$n$角形」や「回転」が絡んだときは複素数平面が非常に有利です．
特に正三角形は東大京大を中心に多くの大学で出題されています．
Aで接しているのでここを原点にとり，まずはDとEの複素数をおきましょう．
この２つと「90度回転」の条件を用いて全ての点を表すことができますから，平行条件の立式をすれば完了です．
複素数平面においては平行条件を「実数倍」と捉えるのではなく，以下のように共役複素数を用いて表現すると楽に（他に文字を置くことなく式だけで）扱えます．（$k$を実数とします）
\begin{align*}
&ABとACが平行\\
\Leftrightarrow\,&\beta-\alpha=k(\gamma-\alpha)\\
\Leftrightarrow\,&\frac{\beta-\alpha}{\gamma-\alpha}=k（実数）\\
\Leftrightarrow\,&\frac{\beta-\alpha}{\gamma-\alpha}=\overline{\frac{\beta-\alpha}{\gamma-\alpha}}
\end{align*}
解答
点Aを原点とする複素数平面で考える。Eを表す複素数を$z_1$，Dを表す複素数を$2z_2$とし，$|z_1|=|z_2|$とする。
$\vec{\mathrm{AB}}$は$\vec{\mathrm{AD}}$を$-90^\circ$，$\vec{\mathrm{AG}}$は$\vec{\mathrm{AE}}$を$90^\circ$回転させたものなので，
\[\mathrm{B}(-2iz_2),\,\mathrm{G}(iz_1)\]
である。ここで，
\begin{align*}
&\vec{\mathrm{EL}}\perp\vec{\mathrm{ED}}\\
&\Leftrightarrow l-z_1=(2z_2-z_1)i\\
&\Leftrightarrow l=(1-i)z_1+2iz_2\\
&\vec{\mathrm{GH}}\perp\vec{\mathrm{GB}}\\
&\Leftrightarrow h-iz_1=(-iz_1-2-z_2)(-i)\\
&\Leftrightarrow h=-(1-i)z_1-2z_2\\
&\vec{\mathrm{EF}}\perp\vec{\mathrm{EA}}\\
&\Leftrightarrow f-z_1=(-z_1)(-i)\\
&\Leftrightarrow f=(1+i)z_1
\end{align*}
が成立しているので，
\[l-f=2i(z_2-z_1)\]\[h-f=-2(z_1+z_2)\]
よって，
\begin{align*}
\frac{l-f}{h-f}&=\frac{2i(z_2-z_1)}{-2(z_1+z_2)}\\
&=\frac{z_1-z_2}{z_1+z_2}i
\end{align*}
また，
\begin{align*}
\overline{\left(\frac{l-f}{h-f}\right)}&=\frac{\overline{z_1}-\overline{z_2}}{\overline{z_1}+\overline{z_2}}(-i)\cdots①
\end{align*}
ここで，$|z_1|=|z_2|\Leftrightarrow z_1\overline{z_1}=z_2\overline{z_2}$であり，この値を$r$とおくと，
\begin{align*}
①&= \frac{\frac{r}{z_1}-\frac{r}{z_2}}{\frac{r}{z_1}+\frac{r}{z_2}}(-i)\\
&=\frac{z_2-z_1}{z_2+z_1}(-i)\\
&=\frac{z_1-z_2}{z_1+z_2}i
\end{align*}
となる。よって，
\[\frac{l-f}{h-f}=\overline{\left(\frac{l-f}{h-f}\right)}\]
から，$\dfrac{l-f}{h-f}$は実数であり，H, F, Lは一直線上にある。