もくじ
解答解説
問題
$x$の整式で表された関数$P(x)$は,次の条件を満たしている.
(i) $P(1)=1$
(ii) すべての実数$x$に対し,$\displaystyle x\int^x_1 P(t)dt=(x-2)\int^{x+1}_1P(t)dt$
このとき$P(x)$を求めよ.
整式と積分方程式の問題です.
整式は次数が$0$以上の整数である式のことを指します(故に定数でも整式).多項式も同義と考えて良いでしょう.
次数に整数条件が絡んでいますから,整式の問題は次数を絞り込みにいくのが大原則です.
関してすでに$0$以上という条件はありますから,次数を上から評価することを目標にします.
本問もその方針で考えてもらえればいいのですが,積分方程式(関数方程式)の形になっていることに着目した人はいますでしょうか.
以前関数方程式,恒等式の問題(それも早稲田でしたね)でお話したように
- 数値代入
- (整式なら)係数比較
- (微分可能なら)両辺を微分する
が大きな3つの方針になります.今回は係数比較が可能な整式ですから,これをメインに考えるべきかと思います.
しかし,積分に引っ張られて微分を考えた人もいるのではないでしょうか?
実際に微分してみると
一回目
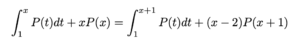
二回目
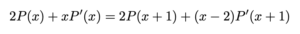
となって,あまり綺麗な形になりません.
このあと次数を決めて係数比較するくらいなら,微分した意味はあまりないですよね.
というわけで,$n$次の整式として係数比較を行ってみましょう.

このようにして,(ii)式について右辺と左辺の同次の項を大きい次数から順に比較していきます.
基本的に欲しいのは次数の情報なので,最高次から注目して行くのですね.
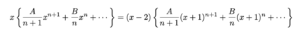
積分されて一次式がかけられているので,最高次は$n+2$次の項となります.
$n+2$次について考えると,右辺も左辺も係数が$\displaystyle\frac{A}{n+1}$となりました.
つまり$n$や$A$の値にかかわらず成立していますから,ここから得られる情報はありませんね.
では次の次数$n+1$の項について調べましょう.ちなみに$n$を$1$以上としたので,$n+1$次は$2$次以上の項です.(よって,$F(1)$の項はこの係数比較に関与しません)
すると,左辺は$\displaystyle\frac{B}{n}$右辺は$\displaystyle A-\frac{2A}{n+1}+\frac{B}{n}$となりますから,$A\neq0$より$n=1$と決まってしまいました.
次数が決まればあとは簡単です.再度$Ax+B$と置き直して$A$と$B$を求めましょう.
以上が一般的な解答の流れになると思います.しかし,もう一つ綺麗な解法を紹介します.
上では原子関数をおきましたが,次は部分積分$\displaystyle Q(x)=\int^x_1 P(t)dt$をおきます.
当然整式の積分も整式になりますから,こちらの方が式がスッキリと書けますね.
さらに,数値代入をすることで$Q(x)$を$0$にする値を見つけることができるので,因数定理から$Q(x)$の持つ因数を把握することができます.
以下の解答はマスターすべきとは言い切れませんが,整式が整数っぽく扱えると言われる意味がよく分かると思いますし,簡潔で個人的にお気に入りなので本解としておきます.
(実際に解くとなれば係数比較で十分だと思います!)
解答
\[\displaystyle Q(x)=\int^x_1 P(t)dt\]とおくと,$Q(1)=0$である.
さらに,(ii)の式に$x=1$を代入すると,
\[\displaystyle\int^2_1 P(t)dt=0\]
であるため,$Q(2)=0$が成立する.
$P(x)$が整式のとき$Q(x)$も整式であるため,$(x-1)(x-2)$を因数に持ち,整式$R(x)$を用いて
\[Q(x)=(x-1)(x-2)R(x)\]
と書くことができる.
(ii)の式は
\begin{align*}
&xQ(x)=(x-2)Q(x+1)\\
&x(x-1)(x-2)R(x)\\
&=(x-2)x(x-1)R(x+1)
\end{align*}
となるため,$R(x)=R(x+1)$が恒等的に成立し,$R(x)$は定数である.
$Q(x)=A(x-1)(x-2)$とおくと,$P(x)=Q'(x)=A(2x-3)$であるが,条件(i)より$A=-1$
よって\[P(x)=-2x+3\]

