short summary!
合同式の性質と式変形に慣れる
「余りを代入する」計算から「除外する(不成立を示す)」意識を持つ
はじめに
大詰めです.今回は整数の基本3ヶ条の3つ目,剰余系について解説していきます.(3ヶ条の記事を読んでいない場合はこちら(click!)から.)
「剰余」は,無限にある整数を有限個のグループに分けるための道具です.
今まで扱ってきた約数・倍数関係や大小関係は,直接的に「整数を絞り込む」方法でした.剰余はこれら2つとは異なり,間接的に絞り込んでいくことが多いです.
もくじ
剰余系(合同式)の利用
「
約数・倍数関係は「割り切れる」ことに関するもので,剰余系は割り切れないものに関しても考えています.
剰余系はある意味では約数・倍数関係の拡張のようなものと言えるでしょう.
例えば
大事なのは,この3つの集合で「全て」の整数が「被りなく一意に」分類出来ているという点なのですが,この辺には深く触れないでおきます.
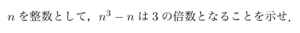
例えばこのような問題の場合
「〜の倍数であることを示せ」という問題で剰余系が威力を発揮するのは当然と言えます.
合同式とは
さて,このように利用価値が高い「剰余」なのですが,「剰余」の計算を簡単にするための道具として「合同式」というものがあります.
「
そして,
modは法(modulo)のことで,「
さて,合同式にはいくつかの性質があります.大事なものを2つ紹介します.
- 負の余りの定義が可能
- 和・差・積の計算が可能
1つめは「余り」の定義についてです.一般的に
基本的に自然数に対してしか割り算や余りの計算をすることはなかったと思いますが,定義することは簡単です.
例えば
と3を足していった形になりますが,当然引いていってもよく,
と書くことができます.負の余りを定義することで,合同式を用いた計算が楽になります.
「3で割った余りは
一般化すると以下のような感じですね.
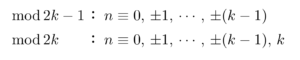
2つ目は,演算についてです.基本的に等式と同じように計算しても良い,ということですね.
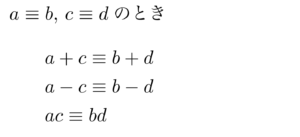
が成立しています.
少し余談にはなりますが,この証明を考えてみましょう,
合同式は余りの計算.ですので,割り算の式を用いて表現できます.
「余りが等しい=差が割り切れる」ですから,
合同式を等式に直す式変形は非常に大事です.ぜひ覚えておきましょう.
特に積の部分が重要で,これを繰り返し用いることで,
(合同式の割り算は条件に制約があります.そもそも割りきれなかったら余りどうこうの問題ではなくなってしまいます.)
剰余系・合同式を用いた絞り込み
基本的な話はここまでです.はじめに「間接的に整数を絞り込む」と言いましたが,どのように使っていくのでしょう.
以下の例題を考えてみてください.
例題
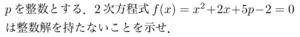
2次方程式ですし,解の公式を使って解いてしまっても正答を出すことが出来ますが,今回は合同式を用いてみましょう.
「ない」ことを示す時は,背理法が便利です.二重否定で肯定的に扱っていきます.
左辺は,
いちいち
実は「矛盾を示す」のが,合同式の得意とするところなのです.
一般的に,等式「
ですから,合同式から等式の条件を得るためには,対偶を考えて,
というわけで,合同式を用いた絞り込みは.「一部の条件を除外する」イメージを持っておきましょう.
今回なら,
例題解答


まとめ
合同式
「余りが等しい=差が割り切れる」
→等式に直すなら
・負の余りの活用
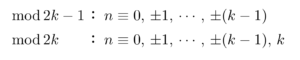
・和・差・積(+累乗)の計算が可能
整数係数の整式
合同式を用いた絞り込みは.「一部の条件を除外する」
直接絞りこむというよりは,削っていくイメージを持つ

