short summary!
二次以上の漸化式は一次の漸化式まで落とすしかない.
まずは①分数式②単項式の2パターンの扱い方を覚えよう.
はじめに
本サイトでは以下のロードマップに従って漸化式を解説していきます.
「解くことの可能な」漸化式に関してはこれで必ず解けます.
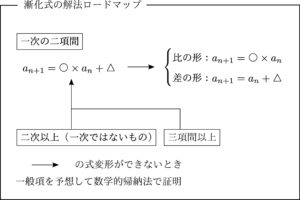
「○次」:一般項($a_n$)がいくつかけられているか
「○項間」:一般項($a_n$)が何種類あるか
で分けていきます.今回は3つ目,二次以上の化式について解説します.
二次以上の漸化式…と聞くとなかなか手強そうに聞こえますね.
でも安心してください,こちらもいくつかのパターンがあるので,それを押さえることでほとんどの問題に対応できます.
もくじ
二次以上の二項間
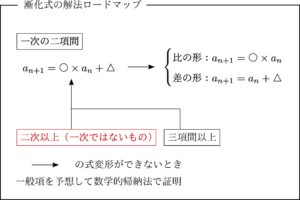
上のロードマップで赤で示したところです.
二次の漸化式とは書いていますが,要は「一次ではないもの」と考えてもらえれば良いでしょう.
例)
$\displaystyle a_{n+1}=\frac{2a_n-5}{3a_n+2}$
$a_{n+1}=3{a_n}^2$
$a_{n+1}=2\sqrt[3]{{a_n}^2}$
といったものです.
解き方はロードマップに書いてある通りで,一次の二項間漸化式$a_{n+1}=○\times a_n+△$まで式変形をしていきます.
まずは基本の2つ①分数式と②単項式の解き方を押さえましょう.
その上で,③その他の変形(因数分解や平方完成など)を見ていきます.
①分数式と②単項式以外のものは基本的にかなり解きづらく,誘導がつくか,そもそも解けないことばっかりです.身構えないでくださいね.
分数式の漸化式
「分数型漸化式」と巷では呼ばれたりします.
特に一次分数式の形になる漸化式について扱っていきましょう.(他のものはそう簡単に解けません)
分数で書かれた漸化式を$a_{n+1}=○\times a_n+△$という形にしたいのです.
しかし,普通の加減乗除ではなかなかそのようにはなりません.
「両辺の逆数をとる」しか方法がないのです.いくつか例を見ていきましょう.
初項は全て$1$とする.
① $\displaystyle a_{n+1}=\frac{a_n}{3a_n+2}$
② $\displaystyle a_{n+1}+1=\frac{a_n+1}{3a_n+2}$
③ $\displaystyle a_{n+1}=-\frac{2a_n+1}{3a_n+2}$
逆数を取るためには「分母は$0$にならない」という大前提をクリアする必要があります.
$0$にならないことを示したければ(否定の証明なので)背理法が楽ですね.
① $\displaystyle a_{n+1}=\frac{a_n}{3a_n+2}$
$a_{n+1}=0$とすると,漸化式より$a_n=0$である.これを繰り返すと$a_1=0$となるが,これは初項が$1$であることに矛盾する.よって任意の$n$について$a_n\neq0$である.
↑この議論はそのまま覚えてしまいましょう.汎用性が高いです.(残りの問題でもほぼコピペで行きます…)
さて,逆数をとっても良いことが保証されましたので,早速式変形していきましょう.
$\displaystyle a_{n+1}=\frac{a_n}{3a_n+2}$
$\Leftrightarrow \displaystyle\frac{1}{a_{n+1}}=\frac{3a_n+2}{a_n}$
$\Leftrightarrow \displaystyle\frac{1}{a_{n+1}}=2\times\frac{1}{a_n}+3$
となります.逆数の数列を$b_n=\frac{1}{a_n}$と置けば$b_{n+1}=2b_n+3$と一次の漸化式になっていますね.
② $\displaystyle a_{n+1}+1=\frac{a_n+1}{3a_n+2}$
こちらも同じようにやって見ます.
$a_{n+1}+1=0$とすると,漸化式より$a_n+1=0$である.これを繰り返すと$a_1+1=0$となるが,これは初項が$1$であることに矛盾する.よって任意の$n$について$a_n+1\neq0$である.
「$a_n=−1$ではない」という書き方でも良かったのですが,コピペ感を出すためにあえて上のように書きました.(覚えておくと楽だと思ってもらえたでしょうか?)
ここから逆数をとって,
$\displaystyle a_{n+1}+1=\frac{a_n+1}{3a_n+2}$
$\Leftrightarrow \displaystyle\frac{1}{a_{n+1}+1}=\frac{3a_n+2}{a_n+1}$
$\Leftrightarrow \displaystyle\frac{1}{a_{n+1}+1}=-\frac{1}{a_n+1}+3$
となります.逆数の数列を$b_n=\frac{1}{a_n+1}$と置けば$b_{n+1}=-b_n+3$とこれまた一次の漸化式になっています.
では次はどうでしょうか.
③ $\displaystyle a_{n+1}=-\frac{2a_n+1}{3a_n+2}$
この式のまま逆数をとってもうまくいきません.①②との違いがどこにあるのかを考えれば
$\displaystyle a_{n+1}-\alpha=\frac{a_n-\alpha}{□}$
の形にしなくては,逆数の数列$b_n$の置きようがないことに気づけたでしょうか.
分数式において,分母というものはなかなかいじりづらいですよね.ここが分数型の漸化式の厄介なところ.
上のように「$a_n-\alpha$」というかたまりを分子側で作った後で逆数を取ることで,置き換えを成立させているというわけです.
では,どのように$\alpha$を見つけ出せば良いのでしょう.
答えは「特性方程式」です.
$\displaystyle a_{n+1}-\alpha=\frac{a_n-\alpha}{□}$
の式は「$a_{n+1}=a_{n}=\alpha$」のときに両辺が$0$になります.元々の漸化式に代入することでこの条件が利用できる,ということです.
実際にやって見ましょう.
$\displaystyle \alpha=-\frac{2\alpha+1}{3\alpha+2}$
$\displaystyle\Leftrightarrow 3\alpha^2+4\alpha+1=0$
$\displaystyle\Leftrightarrow \alpha=-1,\,-\frac{1}{3}$
となります.このとき本当に$\displaystyle a_{n+1}-\alpha=\frac{a_n-\alpha}{□}$の形になっているか確認して見ましょう.両辺から$\alpha$を引くだけです.
$\displaystyle a_{n+1}+1=\frac{a_n+1}{3a_n+2}$
$\displaystyle a_{n+1}+\frac13=-\frac{a_n+\frac13}{3a_n+2}$
特性方程式は$\alpha$の二次式となります.異なる二解を持つ場合はこのように2つ式が出てきます.
($a_n\neq\alpha$を示した後で)どちらを使って逆数を取ってもらっても結構です.ちなみにこれは②と全く同じ式なのでした.
また裏技として上の二式の辺々を割り算することで
$\displaystyle \frac{a_{n+1}+1}{a_{n+1}+\frac13}=-\frac{a_n+1}{a_n+\frac13}$
と,邪魔な分母を消してしまって一気に比の形まで持っていく方法もあったりします.
単項式の漸化式
「積の漸化式」と呼ばれることもあるみたいです.いくつかの一般項がかけられているということですね.
でもこれは簡単.両辺の対数を取ることで複雑な指数部分を和に変えてしまえば一次の形になります.
いくつか例を見ていきます.
初項は全て$1$とする.
① $a_{n+1}=3{a_n}^2$
② $a_{n+1}=2\sqrt[3]{{a_n}^2}$
どちらも対数を取るのですが,注意点が2つほど.
まず,真数条件です.対数が関わる問題では必ず考えなくてはならないところですね.
両辺が正であることを確認した上で式変形に入ります.
次に,底を何に取るかです.何を底に取っても最終的には同じ答えにたどり着くのですが,計算のしやすさ,ミスが起こりにくいようにすることを意識して選ぶようにしましょう.
具体的に見ていきます.
① $a_{n+1}=3{a_n}^2$
初項が$1$であることと漸化式より,任意の$n$について$a_n>0$である.
↑これもテンプレートでいいでしょう.
正じゃないような値は真数条件のそとにあるので,絶対値を取るなりそこだけ別で扱うなり対処が必要になります.(が,あまり見たことがありません)
これで対数を取れるようになりましたから,後は底を何にするかです.
係数$3$が楽に表せるように,ここでは底を$3$にとると
$a_{n+1}=3{a_n}^2$
$\Leftrightarrow \log_{3}{a_{n+1}}=\log_{3}{3{a_n}^2}$
$\Leftrightarrow \log_{3}{a_{n+1}}=2\log_{3}{{a_n}}+1$
となります.対数の数列を$b_n=\log_{3}{a_n}$と置けば$b_{n+1}=2b_n+1$と一次の漸化式になっています.なお,初項は$b_1=\log_{3}{1}=0$です.
② $a_{n+1}=2\sqrt[3]{{a_n}^2}$
初項が$1$であることと漸化式より,任意の$n$について$a_n>0$である.
この部分は同じです.真数条件をクリアしました.
次に底を決める必要があります.
係数$2$を簡単にするために,底を$2$とすると
$a_{n+1}=2\sqrt[3]{{a_n}^2}$
$\Leftrightarrow \log_{2}{a_{n+1}}=\log_{2}{2\sqrt[3]{{a_n}^2}}$
$\Leftrightarrow \log_{2}{a_{n+1}}=\frac23\log_{2}{{a_n}}+1$
となります.対数の数列を$b_n=\log_{2}{a_n}$と置けば$b_{n+1}=\frac23b_n+1$と一次の漸化式になっています.初項は$b_1=\log_{2}{1}=0$です.
その他の場合
分数式や単項式ではない場合は一旦困ります.誘導がないと厳しいこともしばしばでしょう.
ただ,基本的な考え方は「一次に落とす」ことですから,因数分解できるかどうかを試すのは有効と言えるでしょう.例として以下の様なものがあります.
① ${a_{n+1}}^2=a_{n+1}+{a_n}^2-a_{n}$
② $a_{n+1}={a_n}^2-2a_n+2$【信州大学・後期】
①はできて欲しいですね.移項して$n+1$と$n$を分ければ,因数分解できることに気づくはずです.
$a_{n+1}=a_{n}$なら一旦成立するだろうから因数定理のノリで$a_{n+1}-a_n$で括れるかもなあ,という感じでも良いかと思います.
${a_{n+1}}^2-a_{n+1}={a_n}^2-a_{n}$
$\Leftrightarrow (a_{n+1}-{a_n})(a_{n+1}+a_n+1)=0$
$\Leftrightarrow a_{n+1}=a_n$または$-a_n-1$
次数が二次から一次に落とせるという意味で因数分解は効果的です.
当然,解の公式を用いて$a_{n+1}$について解いてしまっても同様の式が現れます.
②です.これはもうすでに$a_{n+1}$について整理されてしまっていますから,右辺をどういじっていくかが問題になります.
形を見てもらえれば,「単項式」の形に似ていることに気づくでしょうか?$a_{n+1}$が$a_{n}^2$と等式で結ばれているからです.
でも$-2a_{n}$が邪魔.そこで平方完成でまとめてみるとかたまりが見えてきます.
$a_{n+1}={a_n}^2-2a_n+2$
$\Leftrightarrow a_{n+1}=(a_n-1)^2+1$
$\Leftrightarrow a_{n+1}-1=(a_n-1)^2$
$b_n=a_n-1$とおけば,$b_{n+1}={b_n}^2$と単項式になっています.つまりこの漸化式は単項式の形から$-1$だけ平行移動した式なのですね.
ちなみに信州大学の後期試験から引っ張ってきた式です.
以上の様にいくつかの工夫が必要になってきます.この章で一般的に言えることはあまり多くないですが,以下まとめておきます.
分数式・単項式ではない漸化式では因数分解や適切な置き換えを試す.
それでも解けない場合は「数学的帰納法」に頼る.
まとめ
「1次まで次数を落とす」ことを目指す
- 分数式→両辺の逆数をとる両辺が$0$ではないことの確認+特性方程式の利用
- 単項式→両辺の対数をとる真数条件:両辺正の確認
- その他→因数分解や適切な置換を考える

