漸化式全パターン徹底解説①：基本２型

はじめに

「漸化式の解き方」を解説している教科書やサイトはたくさんあります．

しかし，どれも煩雑で場合わけも多く，とても覚えられないと感じる人もいるのではないでしょうか．

ここではっきり言っておきたいのですが，10通りも20通りも型を覚える必要はありません．

無駄な場合わけはせず，できるだけ簡潔にまとめました．

本サイトでは以下のロードマップに従って解説していきます．

「解くことの可能な」漸化式に関してはこれで必ず解けます．

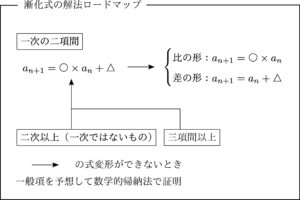
「○次」：一般項（$a_n$）がいくつかけられているか

「○項間」：一般項（$a_n$）が何種類あるか

で分けていきましょう．例を挙げながら説明しますのでわかってもらえると思います．

今回は１回目，漸化式の意味から基本二型について解説します．

漸化式とは

まず，漸化式とはどういうものかを話しておこうと思います．

数列は文字通り「数の列」ですね．初めの数（初項）から数えて$n$番目を構成する数を一般項と呼びます．

一般項を$a_n$とおくと，初項は$a_1$であり，$a_n$で構成される数列のことを$\{a_n\}$と表記するのでした．

ここで，一般項同士の関係式を考えます．

例えば，公差が$3$の等差数列なら，「前の項に$3$を足したものを次の項にする」というルールに基づいて項を定めていきます．

これを一般項を用いて表すと，$a_{n+1}=a_n+3$です．

$a_1=2$などと初項を入れると次の$a_2=5$が出てきて，それをまた漸化式に代入すると$a_3=8$と順々に項が出てきます．

このように，それまでの項を用いて次の項が順々に出てくる構造を漸化式と呼んでいます．

（「漸く」は「ようやく」と読みます．「だんだん」「徐々に」という意味があるのです．枕草子で「やうやう白くなりゆくやまぎは」という文がありますが「やうやう」も「漸う」と表記します．「だんだん白くなっていく山際」ですね．）

漸化式は数列の項を生産する工場で，初項を入れると次の項が出荷され，それを工場に戻して入力するとまた次の項が作られて…というイメージを持っておきましょう．

漸化式を解くということ

漸化式は一般項の関係式です．

例えば

$a_{n+1}=3a_n+4$

という漸化式があり，初項が$1$だとします．$a_5$を求めよ，と言われれば何も困りませんね．$a_1$から順に計算するだけです．

ですが$a_{1000}$を求めよ，と言われると話が変わってきます．計算が大変です．

では，漸化式から$a_n=f(n)$のように一般項を$n$の式として表すことはできないでしょうか．「漸化式を解く」とはまさにこのことです．

本記事では「基本二型」の漸化式から「一次の二項間型」の順に解説をします．

基本二型：「差の形」「比の形」

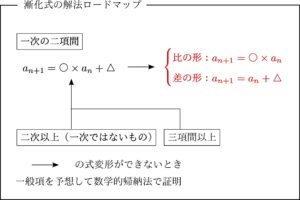
では，上のロードマップにおいて赤で示した「差の形」と「比の形」について解説をしていきます．

数列の基本二型と言われれば，ピンとくるのではないでしょうか．

そうです，等差数列と等比数列です．

について，試しに漸化式を立ててみてください．前の項に何をしたらいいのか…を考えると明白ですよね．

となります．ここでもう一度言及しておきますが，漸化式はあくまでも次の番号を生成する機構ですから，初項の情報は別で必要です．

逆にいうと，

$a_{n+1}=a_n+d$

$a_{n+1}=r\times a_n$

という形なら，それぞれ等差数列，等比数列として一般項を求めることができるということ．

ですが，別に「等しい」差や「等しい」比でなくても，漸化式から一般項を求めることは可能なのです．

例えば，$a_{n+1}=a_n+n$という漸化式を考えてみましょう．

$a_{n+1}$から漸化式を遡るような形で繰り返し用い，$a_1$まで番号を下げてみてください．

$a_1$を代入できれば$a_{n+1}$がわかるということですね．

「差」が与えられている漸化式はこのように一般項を求めることができるのです．

比の場合も同様に考えてもらえれば，以下のようにまとめることができます．

$a_1$まで遡るために「差」には「足し算」を，「比」には「掛け算」をしていくわけです．

なお，上で挙げた例は$a_{n+1}-a_n=n$と書くことができますが，$a_{n+1}-a_n$には階差数列という名前がついています．

これについてはまた別の記事で扱いますのでぜひ参照してください．階差数列から一般項を求める公式も（上で書いてあることとほとんど同じですが）紹介します．

さて，ここで一つ注意して見てほしいのは添字の範囲です．$n$は自然数ですから$n+1$は$2$以上の整数．つまり$a_2$から上の番号に対してのみ成立するということ．

$n$が$1$からスタートすることを考えてもらえればわかると思います．

添字の範囲に迷ってしまったら，「スタートがどこなのか」に注目すると間違えることが減るかも知れません．

よく市販の問題集の解答を見ると，一般項を求めた後に「これは$n=1$でも成立するので」という文言が書かれているでしょう．

これは$a_2$以上のものを表した一般項の式が，$n=1$の時も成立することを確認するためなのです．

ここまで読んできてもらえれば気づいているかも知れませんが，あくまで漸化式は次の項を生成する機構なわけですから

解いた漸化式が初項もきちんと表せているかどうかは当然分からないんですね．

そういう意味では，漸化式を解いた後に「$n=1$でも成立するかどうか」を確認するのは当たり前の作業ということになります．

しかし，この作業を省くことができるものがあります．それが「等差数列」と「等比数列」です．

この二つは「初項」と「公差または公比」で（初項も含めて）一般項を表しきることができるからです．

では，以下の例題を考えてみましょう．

(1)と(2)はいいでしょう．初項と公差，公比が分かっていますから，それぞれ一般項が立てられるはず．

この場合は初項も含んだ状態で答えられるので，$n=1$の時を確認する必要はありません．

問題は(3)と(4)ですね．

漸化式を繰り返し用いて番号を下げることを考えます．

(3)は，見やすいように$b_n=3n^2-n$とすると，

を計算すれば良いということになります．

(4)も同様に

を計算すればokです．

これで得られた式は$a_{n+1}=$という式になっているはずなので，$a_n$になるように番号を一つずらしてあげます．

その際に$n$の定義域が「$1$以上」から「$2$以上」に変わり，「$n=1$の時に成立するかどうか」の確認作業が入る．という段取りです．

まとめ