定義から紐解く有理数と無理数

はじめに

有理数と無理数を初めて習ったのは中学生の時のはずです．

でも「整理して説明せよ」と言われたら詰まってしまう人も多いのではないでしょうか．

実は，定義から順を追って理解すれば問題はワンパターン．

分量が多くなってしまいましたが，しっかり覚えていきましょう！

定義：有理数と無理数

まずは定義からです．ここが全ての肝になりますから必ず押さえましょう．

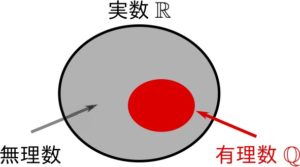
無理数は「（実数に対する）有理数の補集合」として定義されます．有理数があって初めて定義できるものなのです．

雑談ここから~~~~~~~~~~

有理数は英語で"rational number"です．rationalには「合理的な」という意味があります．こちらの訳が色濃く出ていますね．

ですが，これは本来の有理数の意味とは異なります．

ratioは「比」という意味で（等比数列の公比でしばしば用いられる$r$）これは有理数が整数の比で表現される数であることを示唆しています．

「合理的な数」よりも「比の数」が定義としてはしっくりきますね．（誤訳かどうかは意見の分かれるところですが…）

ちなみに無理数は"irrational number"です．接頭辞のirは否定を表しています．

有理数は比の数，無理数は実数における有理数の否定，であることがわかりやすいですね．

雑談ここまで~~~~~~~~~~
（長くてごめんなさい！）

有理数と無理数の基本方針

有理数は，整数の比です．だから，「有理数」が条件に与えられている問題は，整数問題なのです．

整数は強い条件でしたね？積極的に利用しましょう．

また，$\frac12$を$\frac36$や$\frac{-1}{-2}$と表すのは無駄足ですから，

「互いに素」（約分した！ということ）
「分母は正」（正負は分子に委ねる！ということ）

という条件を加えておきます．

この置き方，非常に非常に大事です．特に「互いに素(click!)」は整数の中でも強力な条件です．（リンクから確認してください）

$\displaystyle「=\frac{q}{p}$ （$p,\,q$は互いに素な整数，$p\geq1$）」

これを今すぐメモ用紙に3回書いて覚えてましょう．損はさせません．

例題

有名事実です．高次方程式を因数分解する時には最高次係数と定数項をみますね．その根拠を証明しましょう．

まず，有理数解なので，

$\displaystyle「=\frac{q}{p}$ （$p,\,q$は互いに素な整数，$p\geq1$）」

これですね．解なのでまずは代入してみましょう．

使う条件は$p$と$q$の整数条件，特に「互いに素」です．

互いに素な2数が等号で結ばれている…

「互いに素(click!)」で解説した通り，$p$と$q$の素因数を全て$a_n$と$a_0$に委ねてあげましょう．

これが少し難しかった人は，→互いに素の演習で易しいver.を扱っていますから，そちらを参照してください．

さて，次は無理数条件の利用です．

無理数は定義に否定を含みます．否定を含むものは背理法(click!)との相性がよいのです．

背理法を使う時，示すのはいつも同じで「矛盾」．

無理数と矛盾するものは有理数．定義から明らかですよね？

「（無理数）$=$（有理数）の形」で矛盾を導くことを覚えておきましょう．

以下の例題を考えてください．

無理数の相等と呼ばれるものです．

「（無理数）$=$（有理数）の形」で矛盾を導く

ことが分かっていれば何の問題もないはずです．

ちなみに，「有理数は四則演算の結果が有理数となる（閉じている）」ことを用いています．

無理数であることの証明に関しては↓の記事で扱っています．

ここまでの内容が分かっていればそんなに難しくありませんよ．

まとめ

今回扱った例題はどちらも覚えておく価値があります！