もくじ
解答解説
問題
存在命題の証明です.
考えるべきは
- 具体的な要素をあげる
→ 何か1つ見つけてくる - 「どこかには存在する」ことを示す
→ 中間値の定理,部屋割り論法,平均値の定理 - 背理法
といったところです.以下の記事も参考にしてください.
-

-
「存在」命題の証明法5パターン
short summary! 存在命題の証明は5手覚える. 1具体的に要素を挙げる 2中間値の定理 3平均値の定理 4部屋割り論法 5背理法 はじめに 存在命題は,名前の通り「存在」に関するもので,全 ...
続きを見る
今回の問題は,かなり抽象的な図形の問題.
抽象的な場合は考えにくいため,(図形問題でも関数の問題でも)具体的なイメージを持つことが題意を掴む上で大事になってきます.
各面が合同な鋭角三角形になるような四面体を一度書いてみて…見えてきますか?直方体の存在が
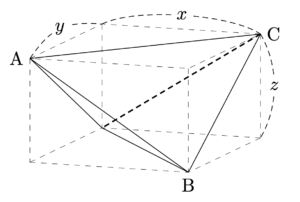
全ての面(4面)が等しい四面体は等面四面体と言います.
対辺が等しく,直方体に埋め込むことができるのが特徴です.
【解答】では唐突に直方体を持ち出しています.
「任意の鋭角三角形に対して,埋め込み可能な直方体があれば,上図のように等面四面体が作れました」
という感じ.つまり,具体的に見つけてきたわけです.
普段書いている数学の答案とはニュアンスが違いすぎてびっくりしてしまう人もいるかもしれませんが,これで立派に満点答案.
存在証明を考える上で「題意を満たすものをとにかく1つ見つけてみよう」という感覚はとても,とても大事です.
図形問題では
- 解析的手法→ベクトル,(成分を導入して)座標
- 幾何的手法
という方針があります.
適当に座標をおいてしまうと,文字が多すぎて計算が大変になることがしばしばありますから,個人的にはベクトルから攻め始めることが多い印象があります.
ただ,今回に関してはベクトル も条件式が立てづらく,存在を示すのが大変なのです.
座標を用いれば(xy平面上に3点をおいて残り1点の存在を示す)確かに証明可能ですが,幾何的に存在を示すのが最も簡便です.
また,等面四面体の特別な場合として「正四面体が立方体に埋め込むことができる」ことも重要です.
京大入試ではよく正四面体が出題されてきました.化学の結晶構造などにも応用が効きますから,ぜひ覚えておいてください.
解答
が成立している.よって,
を定義することができる.
となり,同様にして

任意の

