もくじ
解答解説
問題
以下の文章の空欄に適切な数または式を入れて文章を完成させなさい。
(1) $\displaystyle0\leqq\alpha<\beta\leqq\frac{\pi}{2}$かつ$R>0$とする。極座標$(r,\,\theta)$に関する条件
\[0\leqq r\leqq R,\ \alpha\leqq\theta\leqq\beta\]
により定まる図形を$x$軸のまわりに回転させて得られる立体の体積を$T$とする。$T$を$\alpha,\,\beta,\,R$を用いた式で表すと
\[T=(あ)\ \] である。
(2) 極方程式$r=f(\theta)\ (0\leqq\theta\leqq\alpha)$で表される曲線$C$と,$\theta=\alpha$で表される直線$l$および$x$軸の正の部分で囲まれた図形を$S$とする。ただし$0<\alpha<\displaystyle\frac{\pi}{2}$とし,関数$f(\theta)$は連続かつ$f(\theta)>0$をみたし,$0\leqq\theta\leqq\alpha$において増加または減少または定数とする。
$S$を$x$軸のまわりに回転させて得られる立体の体積を$V(\alpha)$とすると,(1)における$\beta$を$\alpha$に近づけることで,
\[\frac{d}{d\alpha}V(\alpha)=(い)\]
が得られ,したがって
\[V(\alpha)=(う)\]
である。
(3) (2)において$f(\theta)=\sqrt[3]{\cos\theta}$とするとき$\displaystyle V\left(\frac{\pi}{4}\right)$の値を求めると
\[V\left(\frac{\pi}{4}\right)=(え)\]
である。
回転体の体積がテーマの問題です.
しっかり読んで,順番通りに計算を進めるだけ(個人的には京大の理科のイメージと同じです)なのですが,(2)で導関数をきちんと求めることができたかが分かれ目でしょう.
ちなみに,極座標の回転体の公式が,(う)のところの答えです.
この問題のように導出しても良いのですが,覚えるのであればより簡単な方法があるのでお教えします.
パップスギュルダンの定理
断面積$S$が一定の回転体の体積
=$S\times(Sの重心が移動した距離)$
が成立しています.
極座標表示で$(r,\,\theta)$のとき,微小面積を三角形と近似すると$\Delta S$は$\dfrac12r^2 d\theta$とかけます.
さらに,三角形の重心は中点を$2:1$に内分しますから,$x$軸回転させた時には$2\pi\times \dfrac{2r}{3}\sin\theta$だけ移動しますから,パップスギュルダンの定理より
\[\int (2\pi\times \dfrac{2r}{3}\sin\theta)\times\dfrac12r^2 d\theta\]となるわけです.これが(う)と一致します.
解答
(1)
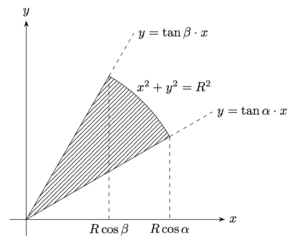
図の斜線部を$x$軸のまわりに回転させると,
\begin{align*}
T=&\pi(R\sin\beta)^2\cdot R\cos\beta\cdot\frac13\\
&+\int^{R\cos\alpha}_{R\cos\beta}\pi(R^2-x^2) dx\\
&-\pi(R\sin\alpha)^2\cdot R\cos\alpha\cdot\frac13
\end{align*}
ここで,
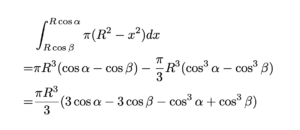
である。代入して,
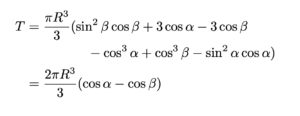
と表せる。よって,
\[(あ)=\frac{2\pi R^3}{3}(\cos\alpha-\cos\beta)\]
(2)
(1)の結果より,
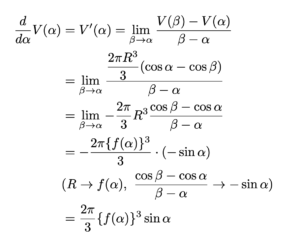
と表される。よって,\[(い)=\frac{2\pi}{3}\{f(\alpha)\}^3\sin\alpha\]
したがって,
\begin{align*}
V(\alpha)&=\int^{\alpha}_{0} V'(\theta) d\theta\\
&=\frac{2\pi}{3}\int^{\alpha}_{0} \{f(\theta)\}^3\sin\theta d\theta
\end{align*}
であるので,\[(う)=\frac{2\pi}{3}\int^{\alpha}_{0} \{f(\theta)\}^3\sin\theta d\theta\]
(3)
(2)の結果より,
\begin{align*}
V\left(\frac{\pi}{4}\right)&=\frac{2\pi}{3}\int^{\dfrac{\pi}{4}}_{0} \cos\theta\sin\theta d\theta\\
&=\frac{\pi}{3}\int^{\dfrac{\pi}{4}}_{0} \sin2\theta d\theta\\
&=\frac{\pi}{3}\left[ -\dfrac12\cos2\theta\right]^{\frac{\pi}{4}}_{0}\\
&=\frac{\pi}{6}
\end{align*}
よって,
\[(え)=\frac{\pi}{6}\]

