もくじ
解答解説
問題
平面上に点Oを中心とする半径1の円$C$がある。また，この平面上のOと異なる点Aを通って直線OAと垂直な空間直線$l$があり，平面とのなす角が45$^\circ$である。このとき，円$C$と直線$l$の間の最短距離を，2点O,A間の距離$a$で表せ。
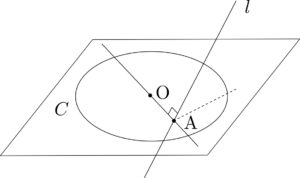
東大は比較的空間図形の出題が多いです．受験する上で必ず対策をしておくべき範囲でしょう．
空間に限らず，図形問題では
- 解析的手法→ベクトル，（成分を導入して）座標
- 幾何的手法
というアプローチを考えるんでした．
平面だと，ベクトルと座標の間として複素数平面（極座標的な立ち位置）も考慮します．
本問は空間ですから，幾何的に考えるとすると断面や射影をとることで二次元に落とす必要があります．
円や$45^\circ$を扱い，さらには距離の最小値を考える上では解析に劣ると考えるべきです．
ベクトルを用いても構わないのですが，まずどのようなベクトルを取ってくるか少し迷いどころ．
$45^\circ$という条件がもっとも扱いやすいのは座標を置くことで，この方針を取れれば後は答えまで一本道でしょう．
空間内の直線は方向ベクトルを用いたパラメータ表示で表す，という原則通りに$l$上の点をおいてしまいましょう．
次に最小値に関してです．はじめに考えるべきは図形の自由度，つまり実質的に幾つの変数が図形を決めているか？ということでしょう．
直線上と円上を独立に動く2点の距離なので，当然2変数関数が出てきます．この程度なら処理できるでしょうか．
また最大最小の記事でお話ししますが，正攻法で扱うのであれば１文字固定で１変数関数として値域を考えにいきます．
$t$と$\theta$を見比べて，明らかに$\theta$の動きの方が面倒ですから，こちらを先に固定して最大最小を求めましょう．
$\cos$の二次関数の形になりますが，極値である頂点が定義域内なのかどうかで場合わけが生じます．この程度ならすんなりとこなして欲しいところです．
解答
空間座標において，円$C$を$x^2+y^2=1,\,z=0$とし，円上の点Pを$(\cos\theta,\,\sin\theta,\,0)$とおく。また，点Aを$(a,\,0,\,0)$とおくと，空間直線$l$上の点Qは$(a,\,t,\,t)$とおける。$(a>0)$
ここで，二点P,Q間の距離$d$は，
$\theta$を固定したとき，$d^2$は$t=\dfrac{\sin\theta}{2}$のとき最小となる。このとき，
\begin{align*}
d^2&=\frac12\sin^2\theta+(a-\cos\theta)^2\\
&=\frac12\cos^2\theta-2a\cos\theta+a^2+\frac12\\
&=\frac12(\cos\theta-2a)^2-a^2+\frac12
\end{align*}
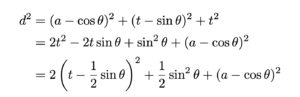
と表せる。
i) $0 < a < \dfrac12$のとき
$d^2$は，$\cos\theta=2a$のとき，最小値$-a^2+\dfrac12$をとる。
ii) $a\geqq\dfrac12$のとき
$d^2$は$\cos\theta=1$のとき，最小値$a^2-2a+1=(a-1)^2$をとる。
以上より，求める最小値は，
\begin{align*}
0<a<\dfrac12\text{のとき}&\displaystyle\sqrt{-a^2+\frac12}\\[5pt]
a\geqq\dfrac12\text{のとき}&|a-1|
\end{align*}