もくじ
解答解説
問題
整数を係数とする
について,次の(1),(2)を証明せよ。
(1) 有理数
(2) ある自然数
方程式
初見ではかなり厳しい問題と言えるでしょう.(1)(2)ともにある程度の知識が必要です.
それでも,(1)の知識は一定のレベルの大学を受けるならば必ず解けるべき問題です.
まず,有理数は
(無理数と関連があり,有理数が加減乗除について閉じていることを用いる場合はこの限りではありませんが,ほとんどの場合は↑で対処します.)
有理数をおいたら,「互いに素」を利用します.ここまで一本道で来れるようにしてください.
- 「肯定」最大公約数が
利用:
証明:最大公約数をおいて,それが - 「否定」共通素因数を持たない
利用:両辺を
証明:共通素因数をおいて,矛盾することを示す
でした.有理数解を代入した場合は,
両辺から
以下に詳しく説明しているのでぜひみてみてください.
-

-
定義から紐解く有理数と無理数
short summary! ・有理数 →分数を代入,整数条件と「互いに素」の利用を意識する ・無理数 →「否定」の利用を意識する はじめに 有理数と無理数を初めて習ったのは中学生の時のはずです. で ...
続きを見る
(2)です.
有理数解を持たないことを直接示すためには,実際に解いて確認するのが一番ですが,こんな方程式が綺麗に解けるわけがないので頓挫します.
「否定の証明」ですから,背理法を使うのが良いでしょう.
有理数解を持つとすると,(1)からこれが整数だとわかります.(1)が使えるのでこの方針で間違いなさそうです.
さてここで整理すると
1.整数解
2.
大まかにこの2つの条件から「矛盾」を示す,ということになります.
割り切れるかどうかという話なので,剰余系を考えますね.
-

-
整数の基本3:剰余系(合同式)
short summary! 合同式の性質と式変形に慣れる 「余りを代入する」計算から「除外する(不成立を示す)」意識を持つ はじめに 大詰めです.今回は整数の基本3ヶ条の3つ目,剰余系について解説し ...
続きを見る
こちらのまとめにも書いている通りですが,剰余系では
- 整数係数の整式
ことを知っておくのでした.
整数係数の整式と剰余系は相性が良いのです.さらに「一部の条件を除外する」というところは背理法と相性が良い.
具体的には
整数に関する深い理解が必要な名問ですね.
解答
(1)
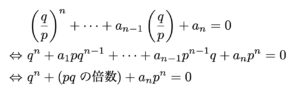
より,
が得られるが,
よって
(2)
方程式
合同式の法
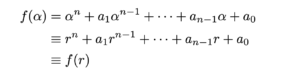
より,
よって背理法により,方程式

