https://mathkoor.site

漸化式全パターン徹底解説②：一次の二項間

2020年7月8日 2020年8月26日

short summary!

一次型の二項間型の漸化式は「比の形」か「差の形」に帰着させる．

はじめに

本サイトでは以下のロードマップに従って漸化式を解説していきます．

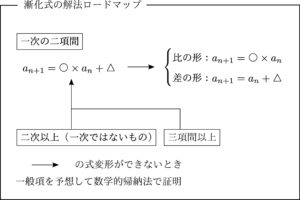
「○次」：一般項（ $a_{n}$ ）がいくつかけられているか

「○項間」：一般項（ $a_{n}$ ）が何種類あるか

で分けていきます．今回は２つ目，一次の二項間漸化式について解説します．

一次の二項間

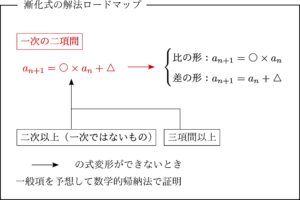
上のロードマップで赤で示したところですね．

一次の二項間漸化式とは， $a_{n + 1} = ○ \times a_{n} + △$ の形をしたものです．

例）

$a_{n + 1} = 3 a_{n} + 2$
$a_{n + 1} = 2 a_{n} + n$
$a_{n + 1} = n a_{n} + 2$

いわゆる一次式のような形をしており，前回の記事で扱った「差の形」と「比の形」の複合ver.といったところでしょうか．

単刀直入に解き方をいうと，「差の形」と「比の形」のいずれかの形に帰着させるのです．

順に扱っていきます．

差の形にする

まずは「差の形」にして見ましょう．

$a_{n + 1} = ○ \times a_{n} + △$ を差の形にするには，○を $1$ にしてやるために何かを両辺にかける必要があります．

実は，これは（後ほど扱う「比の形」よりは）簡単な式変形であることが多いです．

というのも，○に入るのは大体は以下の３通り

①定数

例） $a_{n + 1} = 3 a_{n} + 3^{n + 1}$

② $n$ の一次式

例） $a_{n + 1} = n a_{n} + 2 n!$

③ $n$ の分数式

例） $a_{n + 1} = \frac{n}{n + 1} a_{n} + \frac{2}{n + 1}$

がほとんどだからです．

まずは上に挙げた例についてどのように比の形にするか学んでいきましょう．

① $a_{n + 1} = 3 a_{n} + 3^{n + 1}$

着目すべきは $a_{n + 1}$ と $3 a_{n}$ です．両辺に何かをかけたり割ったりすることで，ここが差の形になるようにしましょう．

$a_{n + 1}$ → $b_{n + 1}$

$3 a_{n}$ → $b_{n}$

を満たすような $b_{n}$ が出てくる式変形をするのです．

係数 $3$ を処理する必要がありますから，両辺を $3^{n + 1}$ で割ることで，

$a_{n + 1} = 3 a_{n} + 3^{n + 1}$

$\Leftrightarrow \frac{a_{n + 1}}{3^{n + 1}} = \frac{a_{n}}{3^{n}} + 1$

となります． $b_{n} = \frac{a_{n}}{3^{n}}$ とすれば $b_{n + 1} = b_{n} + 1$ と差の形になっています．

大体の様子は掴めたでしょうか？この調子で残り２つも差の形にしていきましょう．

② $a_{n + 1} = n a_{n} + 2 n!$

着目すべきは $a_{n + 1}$ と $n a_{n}$ です．両辺に何かをかけたり割ったりすることで，ここが差の形になるようにしましょう．

$a_{n + 1}$ → $b_{n + 1}$

$n a_{n}$ → $b_{n}$

$a_{n}$ は $n$ が順々にかけられていくので，階乗 $n!$ が関わっていると予想します．

よって， $n!$ で両辺を割ってみると，

$a_{n + 1} = n a_{n} + 2 n!$

$\Leftrightarrow \frac{a_{n + 1}}{n!} = \frac{a_{n}}{(n - 1)!} + 2$

となります． $b_{n} = \frac{a_{n}}{(n - 1)!}$ とすれば $b_{n + 1} = b_{n} + 2$ と差の形になっています．

③ $a_{n + 1} = \frac{n}{n + 1} a_{n} + \frac{2}{n + 1}$

着目すべきは $a_{n + 1}$ と $\frac{n}{n + 1} a_{n}$ です．

$a_{n + 1}$ → $b_{n + 1}$

$\frac{n}{n + 1} a_{n}$ → $b_{n}$

差の形にするために $n + 1$ 要素を左辺に， $n$ 要素を右辺に移すイメージを持つと，両辺に $n + 1$ をかけることで

$a_{n + 1} = \frac{n}{n + 1} a_{n} + \frac{2}{n + 1}$

$\Leftrightarrow (n + 1) a_{n + 1} = n a_{n} + 2$

となります． $b_{n} = n a_{n}$ とすれば $b_{n + 1} = b_{n} + 2$ と差の形になっています．

なお，差の形にする式変形は簡単ですが，出てくる階差数列をΣ計算する必要があります．

Σ計算のできない式だった場合，それは解けないか，計算間違いをしているということになります．

比の形にする

$a_{n + 1} = ○ \times a_{n} + △$ を比の形にするには，△を消してやらねばなりません．

△を消すにはどのような式変形をすれば良いのか．

それは，

$f (n + 1) = ○ \times f (n) + △$ を満たす $f (n)$ を見つけて辺々引く

という式変形です．一次の不定方程式なんかと同じですね．

・ $a_{n + 1} = ○ \times a_{n} + △$

・ $f (n + 1) = ○ \times f (n) + △$

↓辺々引く（△が消える！）

$a_{n + 1} - f (n + 1) = ○ \times {a_{n} - f (n)}$

$b_{n} = a_{n} - f (n)$ とすれば， $b_{n + 1} = ○ \times b_{n}$

しかし，どうやってこの $f (n)$ を見つけるのでしょう．

うまく見つけられるようにするには，いくつかのパターンを身につけ，慣れていく必要があります．

少し大変ですが，以下の練習に取り組んでみましょう．次の漸化式を比の形に直してください．

① $a_{n + 1} = 5 a_{n} + 8$

② $a_{n + 1} = 2 a_{n} + 2 n^{2} - n$

③ $a_{n + 1} = 4 a_{n} + 3^{n}$

④ $a_{n + 1} = - a_{n} + n 2^{n}$

① $a_{n + 1} = 5 a_{n} + 8$

$f (n + 1) = 5 f (n) + 8$ を満たすような $f (n)$ を予想しましょう．

定数しか出てきませんから，とりあえず $f (n)$ も定数 $α$ と考えて代入すると

$α = 5 α + 8 \Leftrightarrow α = - 2$

となります．この方程式は特性方程式とも呼ばれますね．

これを与式と辺々引くことで

$a_{n + 1} = 5 a_{n} + 8$

$\Leftrightarrow a_{n + 1} + 2 = 5 (a_{n} + 2) \dots ①$

となります． $b_{n} = a_{n} + 2$ とすれば $b_{n + 1} = 5 b_{n}$ と比の形になっています．

なお，これも単なる式の同値変形．

答案には $f (n)$ を求めるくだりを省いて，①のように書いてしまっても構わないのです．

② $a_{n + 1} = 2 a_{n} + 2 n^{2} - n$

$f (n + 1) = 2 f (n) + 2 n^{2} - n$ を満たすような $f (n)$ を予想しましょう．

二次式が足されているので， $f (n)$ も二次式なのではないかと予想して， $f (n) = A n^{2} + B n + C$ とおいてみましょう．

$A (n + 1)^{2} + B (n + 1) + C$

$= 2 (A n^{2} + B n + C) + 2 n^{2} - n$

整理をして係数比較をすると

$A = 2 A + 2$
$2 A + B = 2 B - 1$
$A + B + C = 2 C$

ですから

$A = - 2, B = - 3, C = - 5$ となります．

よって， $f (n) = - (2 n^{2} + 3 n + 5)$ であるので，与式は

$a_{n + 1} = 2 a_{n} + 2 n^{2} - n$

$\Leftrightarrow a_{n + 1} + 2 {(n + 1)^{2} + 3 (n + 1) + 5}$

$= 2 (a_{n} + 2 n^{2} + 3 n + 5)$

と同値変形できて， $b_{n} = a_{n} + 2 n^{2} + 3 n + 5$ とすれば $b_{n + 1} = 2 b_{n}$ と比の形になっています．

なお，このように式が長くなる場合は $f (n)$ で置き換えるとスッキリ見えます． $b_{n} = a_{n} - f (n)$ と書くのですね．

大体の様子は掴めましたか？この調子で残りも考えていきます．

③ $a_{n + 1} = 4 a_{n} + 3^{n}$

$f (n + 1) = 4 f (n) + 3^{n}$ を満たす $f (n)$ は指数関数となりそうです． $f (n) = A \cdot 3^{n}$ とおいて代入してみましょう．

$A 3^{n + 1} = 4 A 3^{n} + 3^{n}$

$3^{n}$ で割ると， $3 A = 4 A + 1$ となり $A = - 1$ と求まります．

よって， $f (n) = - 3^{n}$ と書くことができるので，与式は

$a_{n + 1} = 4 a_{n} + 3^{n}$

$\Leftrightarrow a_{n + 1} + 3^{n + 1} = 4 (a_{n} + 3^{n}))$

と同値変形ができます．

④ $a_{n + 1} = - a_{n} + n 2^{n}$

$f (n + 1) = - f (n) + n 2^{n}$ を満たす $f (n)$ を見つけます．

一次式に指数関数がかけられている形をしていますから， $f (n)$ も合わせて $(A n + B) 2^{n}$ とおいてみましょう．

${A (n + 1) + B} 2^{n + 1}$

$= - (A n + B) 2^{n} + n 2^{n}$

$2^{n}$ で割ると， $2 A n + 2 A + 2 B = (1 - A) n - B$ となります．

係数比較により $A = \frac{1}{3}, B = - \frac{2}{9}$ と求まります．

よって， $f (n) = \frac{1}{9} (3 n - 2) 2^{n}$ と書くことができて，与式は

$a_{n + 1} = - a_{n} + n 2^{n}$

$\Leftrightarrow a_{n + 1} - \frac{1}{9} (3 n + 1) 2^{n + 1}$

$= - {a_{n} - \frac{1}{9} (3 n - 2) 2^{n}}$

と同値変形ができます．

比の形にできてしまえば，一般項はすぐに求めることができます．

（上のように等比数列になる問題の出題頻度が最も高いと思います．）

使い分けの話

さて「差の形」または「比の形」に式変形をする話をしてきたわけですが，どちらを選ぶのが良いのでしょうか．

一度メリットデメリットを整理しておきます．

	メリット	デメリット
差の形	式変形が簡単	その後に行うΣ計算が大変なことがある
比の形	$f (n)$ が見つかればワンパターンで簡単	$f (n)$ を見つけるのが大変なことがある

これらのことを考慮して，便宜上以下のように使い分けをしていくことにしましょう．

まずは差の形になるように両辺に何かをかけてみる

　↓Σ計算がしづらいようなら

比の形になるように $f (n + 1) = ○ \times f (n) + △$ を満たす $f (n)$ を探してみる

とはいえ， $a_{n + 1} = 5 a_{n} + 8$ のような漸化式なら両辺を $5^{n + 1}$ で割るより先に特性方程式を解いて比の形を目指すでしょう．

演習量をしっかり積むことで使い分けに慣れてくると思います．まずはそれぞれの章で扱った例を繰り返し演習して見てください．

まとめ

一次型の二項間漸化式 $a_{n + 1} = ○ \times a_{n} + △$ は差の形もしくは比の形に帰着させる．

・差の形を目指す

→○が $1$ になるように両辺に何かをかける

・比の形を目指す

→△が消えるように $f (n + 1) = ○ \times f (n) + △$ を満たす $f (n)$ を見つけて辺々引く

役に立ったら押して頂けると励みになります！

-数列

はじめに抽象関数に関する問題です．答えの予想はつくのですが，いざ証明するとなると難航すると思います．早稲田大学は学部ごとに特徴があって個人的に好きです．商学部と理工学部が難しいので有名ですが，本問のように教育学部（理数）も面白い出題がされています．今回の問題は，難易度Sです．ますプラの問題演習では，独自でつけた難易度でタグ付け，さらに東大と京大は別でタグ付けをしてあります．見直す際に利用してください．難易度は以下のようにざっくりと３つに分けています． S：特別な知識や ...

2020/9/29

漸化式全パターン徹底解説④：三項間

short summary! 三項間の漸化式は置き換えで二項間まで落とす．まずは一次型の解き方を覚えてイメージを掴む．はじめに三項間漸化式についてお話しします．よくある一次の形をまず完璧に理解しましょう．本サイトでは以下のロードマップに従って漸化式を解説していきます．「解くことの可能な」漸化式に関してはこれで必ず解けます．「○次」：一般項（ $a_{n}$ ）がいくつかけられているか「○項間」：一般項（ $a_{n}$ ）が何種類あるかで分けていきます．今回は４つ目，　三項間漸化式について解 ...

2020/9/4

漸化式全パターン徹底解説③：二次以上（一次ではないもの）

short summary! 二次以上の漸化式は一次の漸化式まで落とすしかない．まずは①分数式②単項式の２パターンの扱い方を覚えよう．はじめに本サイトでは以下のロードマップに従って漸化式を解説していきます．「解くことの可能な」漸化式に関してはこれで必ず解けます．「○次」：一般項（ $a_{n}$ ）がいくつかけられているか「○項間」：一般項（ $a_{n}$ ）が何種類あるかで分けていきます．今回は３つ目，二次以上の化式について解説します．二次以上の漸化式…と聞くとなかなか手強そうに聞こえますね．でも安 ...

2020/9/4

漸化式全パターン徹底解説①：基本２型

short summary! まずは漸化式の意味と構造を理解する．「差の形」「比の形」の漸化式は「繰り返し用いる」ことで一般項を求めることができる．はじめに「漸化式の解き方」を解説している教科書やサイトはたくさんあります．しかし，どれも煩雑で場合わけも多く，とても覚えられないと感じる人もいるのではないでしょうか．ここではっきり言っておきたいのですが，10通りも20通りも型を覚える必要はありません．無駄な場合わけはせず，できるだけ簡潔にまとめました．本サイトでは以下のロードマップに従って解説し ...

2020/8/26

【速習】数列の和・Σ計算

short summary! 公式を確実に覚える →無理なものは階差の形にするはじめに数列の和は，入試問題としてはそこまで難しいものは出てきません．だからこそ，どのレベルの受験生においてもマスターしておかなければいけない範囲です．基本的な問題から応用までしっかり扱っていきましょう．和の記号：Σ まずはシグマ（Σ）という記号の意味，読みかたをおさらいします．まず，Σの上下を見ます．今回なら「 $k = 2$ 」「 $n - 1$ 」と書いてありますね．よって上の式は「 $k$ に $2$ から $n - 1$ を順番に代入 ...

PREV: 「存在」命題の証明法５パターン
NEXT: 漸化式全パターン徹底解説③：二次以上（一次ではないもの）

sato

国公立医学部卒の医師．学生時代から書き溜めた数学のまとめを，無料で使えるオンライン教科書「ますプラ」として発信中．"知識を有機的に結びつける"をテーマとして，大学入試に役立つ数学の解説を書いていきます．

2020/9/28

【難度A】演習11〜東京都立大学・1987年〜

はじめに多項式の集合と写像に関する問題です．集合と言えば数を含んでいるイメージが強いでしょうが，「一次式」全体を集合と捉えて他の多項式との対応関係（＝関数）を考えてもなんら問題ありません．とっつきづらいかもしれませんが… 今回の問題は，難易度Aです．ますプラの問題演習では，独自でつけた難易度でタグ付け，さらに東大と京大は別でタグ付けをしてあります．見直す際に利用してください．難易度は以下のようにざっくりと３つに分けています． S：特別な知識や熟考が必要なもの（入試では ...

2020/10/1

【難度B】演習15〜早稲田大学（商）・2019年〜

はじめに整式を決定する問題です．積分方程式（関数方程式）の形をとっていますが，どこから手をつけるのが良いでしょうか．今回の問題は，難易度Bです．ますプラの問題演習では，独自でつけた難易度でタグ付け，さらに東大と京大は別でタグ付けをしてあります．見直す際に利用してください．難易度は以下のようにざっくりと３つに分けています． S：特別な知識や熟考が必要なもの（入試では解けなくても問題なし！） A：難問（解けるとアドバンテージ） B：典型問題（解けなければディスアドバンテー ...

2020/9/28

【難度B】演習14（理）〜愛知県立大学〜

はじめにたくさんの正方形が登場する問題です．３点が一直線上にあることを示す方法はいくつかありますが，どれを考えるのが得策でしょうか… 今回の問題は，難易度Bです．ますプラの問題演習では，独自でつけた難易度でタグ付け，さらに東大と京大は別でタグ付けをしてあります．見直す際に利用してください．難易度は以下のようにざっくりと３つに分けています． S：特別な知識や熟考が必要なもの（入試では解けなくても問題なし！） A：難問（解けるとアドバンテージ） B：典型問題（解けなければデ ...

2020/9/28

【難度S】演習13〜早稲田大学（教育）・2017年〜

2020/9/28

【難度B】演習12（理）〜名古屋市立大学〜

はじめに極線に関する基本的な問題です．テーマとして知っているかどうか，とった類の問題で，近年はあまり見かけませんがやっておいて損はないでしょう．今回の問題は，難易度Bです．ますプラの問題演習では，独自でつけた難易度でタグ付け，さらに東大と京大は別でタグ付けをしてあります．見直す際に利用してください．難易度は以下のようにざっくりと３つに分けています． S：特別な知識や熟考が必要なもの（入試では解けなくても問題なし！） A：難問（解けるとアドバンテージ） B：典型問題（解 ...

2020/9/28

【難度A】演習11〜東京都立大学・1987年〜

2020/10/1

【難度B】演習15〜早稲田大学（商）・2019年〜

2020/9/28

【難度B】演習14（理）〜愛知県立大学〜

2020/9/28

【難度S】演習13〜早稲田大学（教育）・2017年〜

2020/9/28

【難度B】演習12（理）〜名古屋市立大学〜

2020/9/28

【難度A】演習11〜東京都立大学・1987年〜