short summary!
公式を確実に覚える
→無理なものは階差の形にする
はじめに
数列の和は,入試問題としてはそこまで難しいものは出てきません.
だからこそ,どのレベルの受験生においてもマスターしておかなければいけない範囲です.
基本的な問題から応用までしっかり扱っていきましょう.
もくじ
和の記号:Σ
まずはシグマ(Σ)という記号の意味,読みかたをおさらいします.
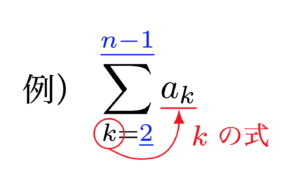
まず,Σの上下を見ます.
今回なら「$k=2$」「$n-1$」と書いてありますね.よって上の式は
「$k$に$2$から$n-1$を順番に代入して足してください」
という命令になります.(ここから$n\geq3$という定義域も得られます)
この「$k$」がΣ計算における変数です.Σの後に続く$a_k$は$k$の式になります.
逆にいうと$k$というのは和を計算するためのローカルな変数なわけです.シグマの中でしか生きることができない.
従って,シグマの計算を終えた後には$k$は登場しません.
「極限」や「積分」でもこうしたローカルな変数は出てきます.どれにも共通して言えるのが上のこと.
良く理解せずに答えに$k$なんて入れた暁には大きな×がついて返ってくるので要注意です.
Σ計算
シグマ計算には公式があります.
- $\displaystyle\sum_{k=1}^n k=\frac{1}{2}n(n+1)$
- $\displaystyle\sum_{k=1}^n ar^k=\frac{ar(1-r^n)}{1-r}\ (r\neq1)$
- $\displaystyle\sum_{k=1}^n k^2=\frac{1}{6}n(n+1)(2n+1)$
- $\displaystyle\sum_{k=1}^n k^3=\left\{\frac{1}{2}n(n+1)\right\}^2$
絶対に覚えるべき公式は赤字にした③④の2つです.
何故なら,①②はそれぞれ「等差数列」「等比数列」の和だからです.
Σ($k$の一次関数)
➡︎等差数列の和の公式
Σ($k$の指数関数)
➡︎等比数列の和の公式
と覚えておきましょう.(当然Σ公式として覚えてもらっても構いませんけどね.)
等差数列と等比数列の和の計算方法に関しては以下の記事を参考にしてください.
-

-
等差数列・等比数列と三項数列
short summary! 等差数列:$n$の一次関数 等比数列:$n$の指数関数 三項数列は真ん中の項に注目 はじめに 今回は数列の基本2つと三項数列(等差中項・等比中項)について学んでいきましょ ...
続きを見る
例題
(1)$\quad 1\cdot n+2\cdot (n-1)+\cdots+n\cdot 1$
(2)$\quad\displaystyle\sum^n_{k=1}\left\{\sum^k_{l=1}\left(\sum^n_{i=1}kl\right)\right\}$
(3)$\quad\displaystyle\sum^{2n+1}_{k=n+1} (-2k+5)$
(4)$\quad\displaystyle\sum^{n+1}_{k=2}2^{2k-3}\cdot3^k$
(1)はまず$\displaystyle \sum a_k$の形に直さなくてはなりませんね.
$k$番目の項は$a_k=k\cdot(n-k+1)$.
$\displaystyle\sum^{n}_{k=1} k(n-k+1)$をどう計算するかが問題です.
ここで先程の変数の話が大事になってきます.あくまでΣ環境の中では変数は$k$です.$k$以外の文字は全て定数とみなします.
$n$はΣの外に出せるというところが分かっていればそこまで難しい問題ではないですね.
(2)も同じところがテーマになっています.
内側のΣから処理していきますが,ここでの変数は$i$です.
中の文字$k,\,l$は定数扱いですから外に出してしまいましょう.残りのΣについても同様です.
(3)(4)は大丈夫ですね.
$k=1$からじゃないから公式が使えない…ではないですよ.それぞれ等差数列,等比数列とみなして和を計算しましょう.
例題解答
(1)
$\displaystyle\sum^{n}_{k=1} k(n-k+1)$
$\displaystyle=(n+1)\sum^{n}_{k=1}k-\sum^{n}_{k=1}k^2$
$\displaystyle=\frac12n(n+1)^2-\frac16n(n+1)(2n+1)$
$\displaystyle=\frac16n(n+1)(n+2)$
(2)
$\displaystyle\sum^n_{k=1}nk\left(\sum^k_{l=1}l\right)$
$\displaystyle=n\sum^n_{k=1}\frac12k^2(k+1)$
$\displaystyle=\frac{1}{24}n^2(n+1)(n+2)(3n+1)$
(3)
初項$-2n+3$,末項$-4n+3$,項数$n+1$の等差数列の和なので
$\displaystyle\frac{1}{2}(-6n+6)(n+1)=3n^2+3$
(4)
初項$18$,公比$12$,項数$n$の等比数列の和なので
$\displaystyle\frac{18(1-12^n)}{1-12}=\frac{18}{11}(12^n-1)$
Σ計算の最終手段
覚えている公式以外の場合はΣ計算できないのでしょうか.
実は,Σの中を「階差の形にする」ことで和の計算ができます.和の中抜け,とも呼ばれるものです.
$\displaystyle \sum a_k$の$a_k$を$f(k+1)-f(k)$(階差)の形に変形します.すると,
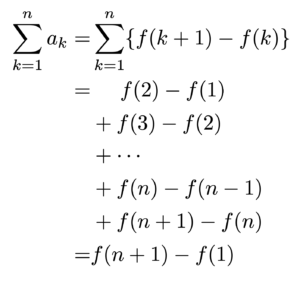
このように両端が残って,中の部分が足し引き$0$になるのですね.
Σ計算の難問において最もよく出てくるところです.
「Σ計算の最終手段は階差形」必ず覚えておいてください.(証明なら数学的帰納法も!)
いくつかお決まりの型があるので,それらを覚えて締めにしましょう.
分数式
→部分分数分解
例)
$\displaystyle \frac{1}{k(k+1)}=\frac{1}{k}-\frac{1}{k+1}$
連続積
→両端に因数を増やす
例)
$\displaystyle k(k+1)=$
$\displaystyle \frac13\{k(k+1)(k+2)-(k-1)k(k+1)\}$
無理式
→分母・分子を有理化
例)
$\displaystyle \frac{1}{\sqrt{k+1}+\sqrt{k}}=\sqrt{k+1}-\sqrt{k}$
まとめ
等差数列・等比数列の公式に加えて$k^2$$k^3$の公式を覚える
公式で求められないものは階差形の利用

