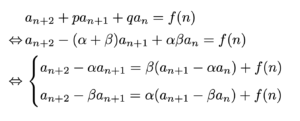short summary!
三項間の漸化式は置き換えで二項間まで落とす.
まずは一次型の解き方を覚えてイメージを掴む.
はじめに
三項間漸化式についてお話しします.よくある一次の形をまず完璧に理解しましょう.
本サイトでは以下のロードマップに従って漸化式を解説していきます.
「解くことの可能な」漸化式に関してはこれで必ず解けます.
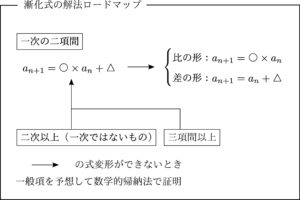
「○次」:一般項($a_n$)がいくつかけられているか
「○項間」:一般項($a_n$)が何種類あるか
で分けていきます.今回は4つ目, 三項間漸化式について解説します.
上では三項間以上の漸化式と書いていますが,やるべことは全く同じ.
まずは一次の三項間漸化式の解き方をマスターして,「二項間漸化式」に帰着させる方法のイメージを掴みましょう.
もくじ
三項間漸化式
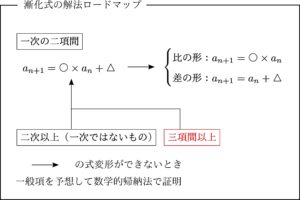
上のロードマップで赤で示したところです.
三項間以上の漸化式とは書いていますが,要は「二項間漸化式ではないもの」と考えてもらえれば良いでしょう.
例)
$a_{n+2}=5a_{n+1}-6a_n$
$a_{n+2}=4\{a_{n+1}-a_n\}$
$a_{n+2}=5a_{n+1}-6a_n+3^{n+1}$
といったものです.$a_n,\,a_{n+1},\,a_{n+2}$という3つの項が入っているので三項間漸化式ですね.
漸化式の1回目でお話しましたが,漸化式は”次の番号を生成する機構”なのでした.
ですから,初期条件として必ず2つ値が与えられます.
$a_1$と$a_2$が与えられて初めて$a_3,\,a_4\cdots$と次々と項が生み出されるということです.
最終目標はロードマップの通り(今までの記事でもやってきた通り)
「置き換え」で(最終的に)「比の形・差の形」へとつなげること
です.
一番基本的な形である一次の二項間漸化式\[a_{n+1}=○\times a_n+△\]まで式変形をしていきます.
三項間のものを二項間にするためには,どのような式変形・置き換えをすれば良いでしょうか.
答えは
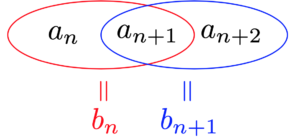
上図のように「$n$と$n+1$」「$n+1$と$n+2$」で組み合わせるのです.
$b_n$が求まったら,$a_n$と$a_{n+1}$について二項間漸化式をもう一回解くことになります.
でもどのように「$n$と$n+1$」「$n+1$と$n+2$」で組み合わせるのかが大問題.
ここからは,最も基本的な形である「一次型の三項間漸化式」について解説していきます.
一次型の三項間漸化式
一般形は
\[a_{n+2}+pa_{n+1}+qa_n=f(n)\]
です.結論から言うと以下のような流れで解いていきます.
- $x^2+px+q=0$の$2$解を$\alpha,\,\beta$と置く.
- 解と係数の関係から$p=-(\alpha+\beta),\,q=\alpha\beta$が成立する.
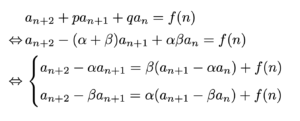
$b_n=a_{n+1}-\alpha a_n$と置くと,$2$項間漸化式$b_{n+1}=\beta b_n+f(n)$が得られる
↓
$b_n$が求まる
↓
二項間漸化式$a_{n+1}-\alpha a_n=b_n$から$a_n$が求まる
もしくは(当然$\alpha$と$\beta$は対称なので)
$b'_n=a_{n+1}-\beta a_n$と置くと,$2$項間漸化式$b'_{n+1}=\alpha b'_n+f(n)$が得られる
↓
$b_n$が求まる
↓
二項間漸化式$a_{n+1}-\beta a_n=b'_n$から$a_n$が求まる
と言うわけで,結果的に二項間漸化式を2つ解いてしまえば答えを求めることができます.
具体的に見ていきましょう.
$a_1=2,\,a_2=3$とする.
①$a_{n+2}=5a_{n+1}-6a_n$
②$a_{n+2}=4\{a_{n+1}-a_n\}$
③$a_{n+2}=5a_{n+1}-6a_n+3^{n+1}$
①$a_{n+2}=5a_{n+1}-6a_n$
まずは$x^2=5x-6$(特性方程式とも呼ばれます)を解くのでした.$x=2,\,3$と求まります.
なんのためにこの方程式を解いたのか分からずに解法だけ覚えてしまう人がいます.
あくまで「二項間漸化式まで落としたい」からだと言うことを忘れないでください.
$x=2,\,3$を用いて,元の漸化式は
\[a_{n+2}=(2+3)a_{n+1}-2\cdot3a_n\]
と書けます.$2a_{n+1}$または$3a_{n+1}$を移項することで
$\begin{cases}
a_{n+2}-2a_{n+1}=3(a_{n+1}-2a_n)\\[5pt]
a_{n+2}-3a_{n+1}=2(a_{n+1}-3a_n)
\end{cases}$
と書くことができます.
答案ではここから書き始めます.これはただの移項であり,同値の式変形なので何も問題ないのです.
私は,この段階で元の式に戻るかどうか必ず確認しています.ここで間違うと一巻の終わりだからです.
さて,これで置き換えが可能になりました.上の式から扱うと,
$A_n=a_{n+1}-2a_n$として,\[A_{n+1}=3A_n\]
$A_1=a_2-2a_1=-1$なので,$\{A_n\}$は初項$-1$,公比$3$の等比数列
よって,$A_n=-3^{n-1}$となる.
$A_n$が求まったので,これを$a_n$の式に代入し,$a_n$を求めます.
$a_{n+1}-2a_n=A_n$
$a_{n+1}=2a_n-3^{n-1}$
である.
ここまで来ればもう大丈夫でしょう.一次の漸化式になりましたから,
- 両辺を$2^{n-1}$で割る
→差の形になる - $f(n+1)=2f(n)-3^{n-1}$をみたす$f(n)$を見つけて引く
→比の形になる
かのいずれかで扱います.本問はどちらの方針でも計算量は大きく変わらないですね.
一次の二項間漸化式については以下で詳しく解説しています.
-

-
漸化式全パターン徹底解説②:一次の二項間
short summary! 一次型の二項間型の漸化式は「比の形」か「差の形」に帰着させる. はじめに 本サイトでは以下のロードマップに従って漸化式を解説していきます. 「○次」:一般項($a_n$) ...
続きを見る
さて,これでめでたく求めることができたのですが,もう一つ便利な解法を紹介します.
$\begin{cases}
a_{n+2}-2a_{n+1}=3(a_{n+1}-2a_n)\\[5pt]
a_{n+2}-3a_{n+1}=2(a_{n+1}-3a_n)
\end{cases}$
先ほどは上の式だけで計算しましたが,下の式も利用すると割と簡単に答えを出すことができる,という話です.
下の式に関して$B_n=a_{n+1}-3a_n$とおくと,\[B_{n+1}=2B_n\]なので,$B_1=a_2-3a_1=-3$と合わせて$\{B_n\}$は初項$-3$,公比$2$の等比数列です.
よって$B_n=-3\cdot2^{n-1}$
ここで,$A_n$と$B_n$を並べてみると
\begin{align*}
&A_n=a_{n+1}-2a_n=-3^{n-1}\\
&B_n=a_{n+1}-3a_n=-3\cdot2^{n-1}
\end{align*}
$a_n$が欲しければ両辺引くことで$a_{n+1}$を消去することができます.
上の式から下の式を引くと$a_n=3\cdot2^{n-1}-3^{n-1}$と求まります.
結果的には漸化式を2つ解いているのですが,こちらの方がより簡単ですね.
一般的に\[a_{n+2}+pa_{n+1}+qa_n=0\]($=0$であることに注意してください)
という形の漸化式に関しては,特性方程式の解を$\alpha,\,\beta$として
\[a\alpha^{n-1}+b\beta^{n-1}\]
の形で一般項が与えられます.
②$a_{n+2}=4\{a_{n+1}-a_n\}$
同様に解いていきましょう.
$x^2=4x-4$の解は重解で$x=2$です.
元の漸化式は
\[a_{n+2}=(2+2)a_{n+1}-2\cdots2a_n\]
と書けます.移項して
$a_{n+2}-2a_{n+1}=2(a_{n+1}-2a_n)$
と書くことができます.
さて,先ほどのように選択肢はなく,このまま置き換えていくことになります.
$A_n=a_{n+1}-a_n$として,\[A_{n+1}=2A_n\]
$A_1=a_2-2a_1=-1$なので,$\{A_n\}$は初項$-1$,公比$2$の等比数列
よって,$A_n=-2^{n-1}$となる.
ここから$a_n$を求めます.
$a_{n+1}=2a_n-2^{n-1}$
一次の漸化式となりましたから,あとは「差の形」もしくは「比の形」を目指しましょう.
今回は両辺を$2^{n-1}$で割ることで差の形にするのが簡単でしょう.
③$a_{n+2}=5a_{n+1}-6a_n+3^{n+1}$
$3^{n+1}$のような変な項が存在した場合にも,方針は変わりません.
まずは三項間を二項間に直すところから着手します.
$a_n$については①と同じ式ですから,以下のように変形できます.
$\begin{cases}
a_{n+2}-2a_{n+1}=3(a_{n+1}-2a_n)+3^{n+1}\\[5pt]
a_{n+2}-3a_{n+1}=2(a_{n+1}-3a_n)+3^{n+1}
\end{cases}$
上の式を用いて置き換えを行いましょう.
$A_n=a_{n+1}-2a_n$として,\[A_{n+1}=3A_n+3^{n+1}\]
この漸化式なら,両辺を$3^{n+1}$で割るのが簡単でしょう.
\[\frac{A_{n+1}}{3^{n+1}}=\frac{A_n}{3^n}+1\]
$A_1=a_2-2a_1=-1$なので,$\{\displaystyle\frac{A_n}{3^n}\}$は初項$-\frac{1}{3}$,公差$1$の等差数列
よって,$A_n=(n-\frac43)3^n$となる.
$A_n$が求まったので,これを$a_n$の式に代入し,$a_n$を求めます.
$a_{n+1}-2a_n=A_n$
$a_{n+1}=2a_n+(n-\frac43)3^n$
である.
この一次型の漸化式を解いていくことになります.
もしくは,①と同じように$a_{n+2}-3a_{n+1}=2(a_{n+1}-3a_n)+3^{n+1}$を解いたものから$a_{n+1}$を消去することで$a_n$を求めます.
まとめ

置き換えで「二項間まで落とす」ことを目指して,「$n$と$n+1$」「$n+1$と$n+2$」で組み合わせる
- $x^2+px+q=0$の$2$解を$\alpha,\,\beta$と置く.
- 解と係数の関係から$p=-(\alpha+\beta),\,q=\alpha\beta$が成立する.