【難度A】演習5〜大阪大学・2010年〜
はじめに 大阪大学の有名な整数問題. 整数について習いたてではなかなか苦戦すると思いますが,しっかり取り組んで欲しい問題です. 今回の問題は,難易度Aです. ますプラの問題演習では,独自でつけた難易度でタグ付け,さらに東大と京大は別でタグ付けをしてあります.見直す際に利用してください. 難易度は以下のようにざっくりと3つに分けています. S:特別な知識や熟考が必要なもの(入試では解けなくても問題なし!) A:難問(解けるとアドバンテージ) B:典型問題(解けなければディスアドバ ...
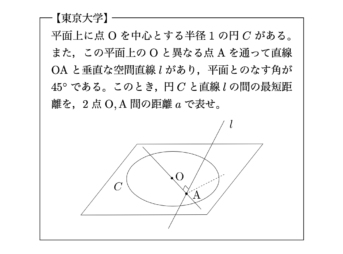
【難度B】演習4〜東京大学・1983年〜
はじめに 東京大学の空間図形の問題. 東大だからとあまり気負わずに取り組んでみてください. 今回の問題は,難易度Bです. ますプラの問題演習では,独自でつけた難易度でタグ付け,さらに東大と京大は別でタグ付けをしてあります.見直す際に利用してください. 難易度は以下のようにざっくりと3つに分けています. S:特別な知識や熟考が必要なもの(入試では解けなくても問題なし!) A:難問(解けるとアドバンテージ) B:典型問題(解けなければディスアドバンテージ) これは主観的な評価で,大 ...
【難度A】演習3〜千葉大学・2010年(後期)〜
はじめに 今回は問題演習編. ますプラの問題演習では,独自でつけた難易度でタグ付け,さらに東大と京大は別でタグ付けをしてあります. 見直す際に利用してください. なお,変に先入観をもたないようにあえて単元やテーマは明示しないようにしています.(カテゴリータグを見れば分かってしまいますが…) 難易度は以下のようにざっくりと3つに分けています. S:特別な知識や熟考が必要なもの(入試では解けなくても問題なし!) A:難問(解けるとアドバンテージ) B:典型問題(解けなければディスアドバンテージ) ...
【難度B】演習2(理)〜慶應義塾大学・2012年〜
はじめに 曲座標における回転体の体積に関する問題です. 慶應の医学部の問題なのですが,やたら長くて大変なものが多く出題されるので読むだけでも一苦労ですよね… 全くもって典型題ではありませんが,誘導に沿って考えていけばそこまで大変ではないはずです. 今回の問題は,難易度Bです. ますプラの問題演習では,独自でつけた難易度でタグ付け,さらに東大と京大は別でタグ付けをしてあります.見直す際に利用してください. 難易度は以下のようにざっくりと3つに分けています. S:特別な知識や熟考が ...
漸化式全パターン徹底解説④:三項間
short summary! 三項間の漸化式は置き換えで二項間まで落とす. まずは一次型の解き方を覚えてイメージを掴む. はじめに 三項間漸化式についてお話しします.よくある一次の形をまず完璧に理解しましょう. 本サイトでは以下のロードマップに従って漸化式を解説していきます. 「解くことの可能な」漸化式に関してはこれで必ず解けます. 「○次」:一般項($a_n$)がいくつかけられているか 「○項間」:一般項($a_n$)が何種類あるか で分けていきます.今回は4つ目, 三項間漸化式について解 ...
【難度A】演習1〜京都大学・1989年(後期)〜
はじめに 格子点が絡んだ京大の難問&良問です. 90年代の京都大学後期はなかなか難問・良問揃いなので当サイトでもたくさん扱っていきます. 今回の問題は,難易度Sです. ますプラの問題演習では,独自でつけた難易度でタグ付け,さらに東大と京大は別でタグ付けをしてあります.見直す際に利用してください. 難易度は以下のようにざっくりと3つに分けています. S:特別な知識や熟考が必要なもの(入試では解けなくても問題なし!) A:難問(解けるとアドバンテージ) B:典型問題(解けなければデ ...
漸化式全パターン徹底解説③:二次以上(一次ではないもの)
short summary! 二次以上の漸化式は一次の漸化式まで落とすしかない. まずは①分数式②単項式の2パターンの扱い方を覚えよう. はじめに 本サイトでは以下のロードマップに従って漸化式を解説していきます. 「解くことの可能な」漸化式に関してはこれで必ず解けます. 「○次」:一般項($a_n$)がいくつかけられているか 「○項間」:一般項($a_n$)が何種類あるか で分けていきます.今回は3つ目,二次以上の化式について解説します. 二次以上の漸化式…と聞くとなかなか手強そうに聞こえますね. でも安 ...
漸化式全パターン徹底解説②:一次の二項間
short summary! 一次型の二項間型の漸化式は「比の形」か「差の形」に帰着させる. はじめに 本サイトでは以下のロードマップに従って漸化式を解説していきます. 「○次」:一般項($a_n$)がいくつかけられているか 「○項間」:一般項($a_n$)が何種類あるか で分けていきます.今回は2つ目,一次の二項間漸化式について解説します. 一次の二項間 上のロードマップで赤で示したところですね. 一次の二項間漸化式とは,$a_{n+1}=○\times a_n+△$の形をしたものです. 例) $a_{ ...
「存在」命題の証明法5パターン
short summary! 存在命題の証明は5手覚える. 1具体的に要素を挙げる 2中間値の定理 3平均値の定理 4部屋割り論法 5背理法 はじめに 存在命題は,名前の通り「存在」に関するもので,全称と対の関係にあります. 「”ある/適切な/適当な”$n$について成立」 「〜を満たすような$n$が存在する」 のようなセリフとして登場します. 今回はこの「存在」が絡んだ証明問題の解法を学んでいきましょう. 存在命題の証明 存在証明は全称命題よりも分かりやすいと思います. 「存在」には「少なくとも1つ」とい ...
「全称」命題の証明法4パターン
short summary! 全称命題の証明は4手覚える. 1最大最小や不等式 2数学的帰納法 3剰余系 4背理法 はじめに 全称命題という言葉を聞いたことはあるでしょうか. 大まかに言うと「全」のイメージで, 「”任意の/全ての/どんな”nについて成立」 のようなセリフとして登場します. 今回はこの「全称」が絡んだ証明問題をどう解き崩していくかを学んでいきましょう. 全称命題の証明 基本的に全称命題の証明は難しいです. 「全ての一桁の整数について示せ」なら0-9までの10個の数を代入してしまえば済む話で ...