もくじ
解答解説
問題
次の$x$に関する方程式が実数解を持たないような負の数$k$の範囲を求めよ。\[\sqrt{x-1}-1=k(x-k)\]
今回は無理方程式に関する問いです．
無理式は大まかに分けて
①グラフで議論を進める
②二乗してルートを外す
の２通りがあります．
本問は，「ルートは二乗」と思い込んでいると痛い目にあう問題ですね．
二乗する際には両辺$0$以上を気にする必要がありますね．移項して$k(x-k)+1\geqq0$を条件においたまま，$x$の二次方程式を考えますか？
さらに，パラメータである$k$が$4$次に跳ね上がってしまい，非常にやりづらかったでしょう．
そもそも「（実数）解の存在」を扱うのですから，グラフで処理を進める①が得策なのです．
無理関数のグラフは放物線．単調性があり扱いやすいことも，①で考える大きな根拠になります．
さて，グラフを書くと言っても，右辺は$k$が$2$次で絡んでいてあまり綺麗ではありませんね．
しかし，$k<0$という条件と$x$一次式なので，「傾き負の直線だ」とざっくり捉えてもらえればそう大した問題にはなりません．
今回は存在”しない”なので，共有点をもたないように動いてもらいましょう．
無理関数は下手に二乗してしまうと「無縁解」と呼ばれる定義域外の解がもとまることが多いです．まずはグラフで処理できるか試すようにしてください．
解答
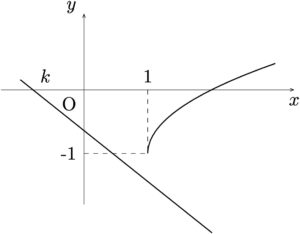
題意より，$x-1\geqq0$なので，$x\geqq1$で考える。$k<0$より，この範囲で曲線$y=\sqrt{x-1}-1$は単調増加であり，直線$y=k(x-k)$は単調減少である。
曲線$y=\sqrt{x-1}-1$と直線$y=k(x-k)$が共有点を持たなければ良いが，上図のグラフと単調性より，この条件は点$(1,\,-1)$が直線$y=k(x-k)$よりも上側にあることである。
よって，\[-1>k(1-k)\]であり，これを解くと，
\[k<\frac{1-\sqrt{5}}{2},\,\frac{1+\sqrt{5}}{2}<k\]
$k<0$より，求める$k$の範囲は，\[k<\frac{1-\sqrt{5}}{2}\]