もくじ
解答解説
問題
を考える.ただし,
(1)
(2)
微分をするだけと言ってしまえばそれまでなので,幾つか注意点を.
まず指数に変数が入っている状態は非常に扱いづらいので対数をとって微分をすること.
さらに,対数を取るのであれば必ず真数条件を確認しましょう.
微分をする時,欲しいのは導関数の符号変化です.符号がすでに分かっているところは適宜除いて計算を進めていきます.
変に
解答
(1)
両辺を微分して,
とおく.
これは
であるため,
以上より,
(2)
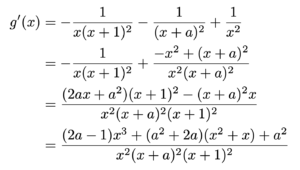
分子について,
であるため,
以上より,

