「存在」命題の証明法５パターン

はじめに

存在命題は，名前の通り「存在」に関するもので，全称と対の関係にあります．

「”ある/適切な/適当な”$n$について成立」

「〜を満たすような$n$が存在する」

のようなセリフとして登場します．

今回はこの「存在」が絡んだ証明問題の解法を学んでいきましょう．

存在命題の証明

存在証明は全称命題よりも分かりやすいと思います．

「存在」には「少なくとも１つ」という意味が含まれていますから，題意を満たすものを１つ見つけてくれればいいわけです．

しかし，難問になると簡単には見つからないものも多く，証明方法として

どこにあるのかはわからないけれどどこかにはありますよ

と言った大雑把な見つけ方をする場合があります．

以上の５手が覚えるべきものです．⑤背理法は，①から④までを考えた結果困ってしまった場合に考えてください．

それぞれについてお話ししていきましょう．

具体的に要素を挙げる

これは先ほどにも書きました通り，

「存在」を示したければ１つ見つけてくれば良い

という考え方です．

一番大事な考え方であるにも関わらず，他のいろんな知識が邪魔して落とし穴になってしまうところ．

「ある$x$について$x^2+3x+1<0$を示せ」

と言われればそれは

「$x^2+3x+1$の最小値$<0$」

です．

とにかく$0$より小さい値を１つ見つけたいので，左辺の一番小さい値を挙げれば問題ないだろう，と考えるのですね．

全称とは違い，どの文字について存在命題なのかが明示されることが多いので，その点では分かりやすいかもしれません．

全称命題の記事で「２変数の問題では領域図示を試す」というお話をしたと思いますが，存在命題でも効果があります．

「①かつ②を満たすような変数$x,y$が存在することを示せ．」

という問題に対して，

「①と②の領域に共有部分がある」と読み替えればokです．

もっと言えば，①②の共有部分の適当な要素$x,y$を提示すれば存在証明として成立していますから，それでも問題ありません．

中間値の定理

中間値の定理は「連続関数における解の存在」を示す際に特に重宝する手法です．

という定理です．

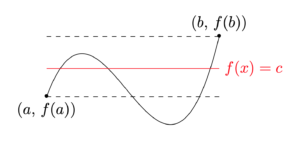
$f(a)$と$f(b)$の間を連続的に動くなら，通り過ぎたり戻ったり色々動いたとしても，図の赤線を超えてしまうよね，と言っています．

逆に連続でなければ，図の赤線をヒョイっと飛び越えて動くこともあり得ますから，上の定理は成立しません．

存在命題の証明あるあるなのですが，これも至極当たり前に感じてしまいますね．

よく出てくるのはグラフの交点＝連立方程式の解の存在です．

二次方程式の解の配置では馴染み深いはず．

絶対値が1の数は$\pm 1$です．解の配置でまず考えなくてはならないのは端点における値

今回で言うと$f(-1),f(1)$です．計算してみると

$f(1)=a-b+c$
$f(1)=a+b+c$

です．与えられた条件よりこれらが負であることが分かります．最高次係数は正なので，グラフの概形は以下のよう．

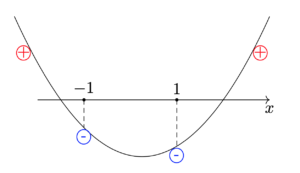
二次関数なので，$x$をずっと小さくしたりずっと大きくすれば正の値になるはず．

マイナスとプラスを連続的に動くためにはその境界である$x$軸を通らなければなりません　←中間値の定理

よって$-1$未満と$1$より大きいところに解が出てくることがわかりました．

厳密に答案を書くなら，見つけた解以外には存在しないことに言及しておきましょう．

このように，「異符号の間を連続に動けば0を通る」の形で解の存在範囲を定めることが多いです．まとめておくと

これを覚えておけば一旦okです．単調なら存在を強めて「唯一」と言えることも知っておきましょう．数Ⅲでよく問われます．

平均値の定理（数Ⅲ）

平均値の定理は，特に微分係数に関する存在証明で用います．

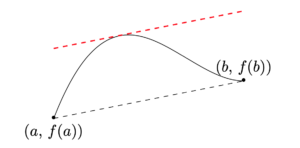
と言う定理です．証明は「ロルの定理」を用いますが，図を見ればなんとなく正しいことは分かると思います．

正直，存在証明の問題よりも，極限や不等式の証明等でお目にかかることが多いですね．

覚えておきたいのは

関数の差の形$f(b)-f(a)$

を見たときに平均値の定理の考えると言うこと．証明も含めて，詳しい話はまた別の機会にしましょう．

部屋割り論法

有限個に分類できるような集合に対する存在命題で用います．

と言うことで，これも数学というよりは当たり前の論理でしょう．

わかりづらければ少ない数で考えてみてください．

３つの巣に４羽の鳩が入ろうとすると，全員がシングルルームで快適に寛ぐことができなさそう，という訳ですね．

頻出の２テーマを押さえておけば，入試に関しては十分と言えるでしょう．

剰余

剰余系は整数全体を有限個の集合に分けられる点で優れています．部屋割り論法において最も頻度が高く，相性もよいです．

例）$5$個の数の中から，その差が$4$で割り切れるような$2$数を選ぶことができる

「部屋」：$4$で割った余り$4$種類
「物」：$5$個の数

距離

距離を有限個区間に区切って，二点間の距離について論じる問題が散見されます．

例）2m幅の道に3本の木を植えると，2本の差が1m以内の木が存在する

「部屋」： 区間$0\le x<1,1\le x\le 2$の2つ
「物」：3本の木

以下の例題にチャレンジしてみてください．

「部屋割り論法をいつ使うのか」と聞かれるとはっきり答えるのはなかなか難しいです．

存在命題と有限集合（有限個の要素）が合わさったときに使えるか試してみましょう．

多くの問題において，「物」の数は与えられています．

(1)なら，「９点」選ぶ訳ですから，もし部屋割り論法を用いるとすれば，「部屋」の数は$9-1=8$個以下でなければなりません．

中点は「足して2で割る」訳ですから，座標が2で割れるか（つまり偶奇）が問題になりますね．

$x,y,z$の偶奇がすべて一致するような組が存在すれば良いので…これで8個の部屋が作れたでしょうか．

(2)も同様，「$n+1$個」選ぶ訳ですから，もし部屋割り論法を用いるとすれば，「部屋」の数は$n+1-1=n$個以下です．

$n$個，と言われると（具体的な数値ではないので）難しく感じるかもしれません．少し実験してみましょう．

$$1,3,\cdots ,2n-1$$

とできるだけ連続整数とならないように数を選ぶと，これで$n-1$個です．

あと一つはどうしても偶数から選ぶ必要が出てきますね．ここで連続なとこが生まれてしまいます．

では，部屋はどのように作ればいいでしょう．$2n$個の数を$n$個の部屋に分けることと，上で実験したことを考え合わされば分かるはずです．

まとめ