必要と十分と必要十分

はじめに

「必要と十分」きちんとわかっていますか？

日本語でもよく使う馴染みのある言葉のはずですが，いまいちよく理解出来ていない人も多いかと思います．

今回は定義から丁寧に解説していきます．しっかり読み込んでもらえれば，この先絶対に混同することはないはずです．

必要と十分とは

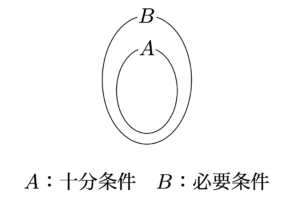
必要と十分は集合の包含関係を表しています．上の場合であれば，BがAを包含していますから，

\[A\Rightarrow B\ \cdots①\]

が成立しています．Aの要素なら全てBを満たすということです．

そして，この図と①の式において，Aのことを十分条件，Bのことを必要条件と呼ぶのです．

さしあたっては「矢の先が必要条件」だと覚えましょう．

それに加えて，上の包含関係に加えて，以下の様なイメージを持ってもらえるといいと思います．

月並みですがいくつか例をあげましょう．

人間であるに対して動物は「少なくとも必要」ですね．

ですが乱雑で弱すぎます，他のものが混じりすぎている．

つまり，BはAに対する必要条件です．矢印で表現するなら$A\Rightarrow B$

また，AとBの場所が入れ替わると必要と十分が入れ替わります．

「BはAに対する必要条件」なら「AはBに対する十分条件」です．

人間であるに対して日本人男性は「念のため十分」ですね．

ですが厳密で強すぎます，限定しすぎで数え漏れがたくさんある．

つまり，CはAに対する十分条件です．矢印で表現するなら$A\Rightarrow C$

また，先ほどと同様に

「CはAに対する十分条件」なら「AはCに対する必要条件」です．

必要十分とは

必要十分は文字通り「必要かつ十分」ということです．

式で表すと，

\[A\Rightarrow B,\,B\Rightarrow A\]

となります．ちなみにこれをまとめて$A\Leftrightarrow B$と表現します．

くどく表現すると「A（B）はB（A）に対する必要条件であり十分条件」となります．

これは過不足のない完全一致状態と言え「同値」とも表現されます．

例えば

「人間である」に対して「ホモ・サピエンスである」は「必要十分」

ですね．問題なく言い換えられています．

実際に問題を解く時には

さて，必要と十分，必要十分については理解できたと思います．

マーク式試験で出てくる様な問題なら，今までの事項を押さえておくだけで必要か十分かの判別がつくでしょう．

しかし，実際に問題を解く，答案を書くとなった時に，必要性，十分性が論点になることがあります．いくつかの事例を挙げながら見ていきましょう．

求値問題「〜を求めよ」の場合

求値問題で大事なのは，条件を必要十分で扱わねばならないということです．

例えば，「方程式を解く」問題で考えてみましょう．

この方程式に対して

「$x=2$を代入すると成立するので，求める答えは$x=2$」

と答えを書くとマルがもらえるでしょうか．

実はこれでは正解とは言えません．というのも，この状況は「十分性しか求めることができてない」からです．

あくまで１つ見つけてきただけで，他の解があるかもしれない，ということですね．

では，「$x=2,\,3,\,5$」と答えた場合はどうでしょう．こちらは明らかに誤っているでしょう．解ではない$x=5$が混ざってしまっています．

この状況は「必要性しか求めることができていない」と言えます．

$x^2-5x+6=0\Leftrightarrow x=2,\,3$

ですから，この二数を答えなくてはなりません．与えられた条件を過不足なく言い換えて答えを求めましょう．

不等式の解（値域や領域図示など）も同じです．示す範囲が足りないのはもちろん，広過ぎても間違いとなります．

証明問題「〜を示せ」の場合

証明問題の場合は，基本的に必要条件のみを示します．

証明問題の流れを考えてもらえればわかると思うのですが，

という構成になっているはずです．$A\Rightarrow B$と表せますよね．これは必要条件を示すことに他ならない．

示したいものが決められていますから，わざわざ必要十分で扱わなくともよいのです．

証明問題の多くが必要性の問題なのですが，必要と十分の違いをよくわかっていないと下に記す様な間違いをしてしまいかねません．

これが間違いであることは分かりますよね？

C「$n=1,\,2,\,3$」は前提条件であるA「自然数$n$」の十分条件に過ぎないからです．

つまり，構造として

CならばA，CならばB：$C\Rightarrow A,\,C\Rightarrow B$

を示したに過ぎず，

AならばB：$A\Rightarrow B$

は全く示せていないというお話です．

「AならばB，BならばC」という三段論法なら合っているんですけどね．

しかし，例外もいくつかあります．「必要十分」を示す様な問題もあるということです．

この場合は，以下の様に問題文にしっかり明示されます．

この場合は，$A\Rightarrow B$のみを示すだけでは不十分となります．

必要十分で扱うためには

必要十分で扱う必要があるのは，

の二通りです．

ここからは，必要十分が関連する項目を挙げながら，どのように扱っていけば良いのかを解説します…

としたいところなのですが，例を挙げだすと大変な分量になってしまったので別の記事にしますね．

まとめ