背理法：論証における「否定」の利用について

はじめに

今回は「否定」特に論証における利用について考えていきます．

背理法は数ある証明の方法の中でもとても強力なものです．是非マスターしましょう！

似ているもので対偶法との違いについても解説していきます．

背理法とは

まずは背理法とは何かというところから．

証明問題では，

「条件Aが与えられて結論Bを示す（$A\Rightarrow B$）」

という構造になっているはずです．

$A\Rightarrow B$において，AはBの十分条件，BはAの必要条件と呼ばれます．

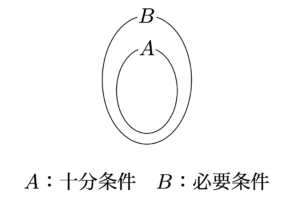
当然Bがどういうものなのかで証明方法は様々です．

しかし，背理法は$A\cap \bar{B}\Rightarrow \varphi$を示します．

「Aの内側」かつ「Bの外側」の領域に何もない，矛盾してしまう．

証明すべきものが「矛盾」と定まっているのが特徴的ですね．

なお，対偶法は$\overline{B}\Rightarrow A$を示す方法ですが，これも集合を考えると

「Bの外側」なら「Aの外側」という意味で図を見ると明らかでしょう．

対偶法も背理法も共に結論の否定を用いますが，証明においては，背理法に軍配が上がるでしょう．

使える条件が$A$と$\overline{B}$である点，「矛盾を示す」と割り切って考えられる点が優れています．

一方で，対偶法に関しては，命題を同値変形して扱いやすくするのに長けています．

「AならばBが成立する時，〜となる条件を求めよ」と言った問題は証明ではないので背理法は使えませんね．

こうした場合は対偶法の出番です．

否定の利用を考える

に特に背理法（対偶法）・余事象を考えましょう．

とはいえ，一見しただけでは場合わけが多いかどうかの判別ができないものもあります．

命題は常に否定したものと一緒に考えて，扱いやすい方を選ぶというアプローチが得策と言えるでしょう．

①場合分けを多く含む時は，その否定は少ない場合分けで済むはず，という考え方です．

「少なくとも1つはA」の否定は「1つもAではない」

「AまたはB」の否定は「AではなくかつBではない」

なので扱いやすくなっていますね．

②否定を含む時は，もう一度否定（二重否定）することで肯定に戻せば扱いやすくなるはず，という考え方です．

それぞれの例を見ていきます．

・場合分けを多く含む命題

「$a,b$のいずれか」が背理法の利用を思い浮かべるヒントです．

結論の否定「$a,b$のいずれも3の倍数ではない」と与えられた条件「$a^2+b^2=c^2$」を組み合わせて矛盾を作ってみましょう．

3の倍数ではない，ということは余りが出るということですから，剰余系の利用が思いつけば正答にたどりつけるはずです．

・否定を含む命題

以下のものはよくある問題ですので，背理法の使い方として暗記してしまって損はありません．

〜無理数の証明〜

無理数は「有理数ではない実数」です．有理数は扱いやすい数ですから，こちらを使いたい，と考えます．

有理数と無理数に関しては↑も参考にしてください．

(1)は①を用います．無理数の条件がないからですね．

有理数とおいた場合は互いに素に矛盾させにいきます．分母分子の共通素因数を見つけてくれば良いのですね．

(2)は(1)の無理数条件が使えますから，$\alpha =$（有理数）の形の矛盾を作りにいきます．

〜素数が無限に存在することの証明〜

無限は扱いづらいですが，その否定「有限」は扱いようがあります．

とはいえ有限性の利用は少し難易度が高いですね．

有限なら「最大・最小」が存在する

ことを，今回の例題から学んでください．

素数を有限個と仮定してみましょう．最大の素数が存在しますね．

「最大の素数」に矛盾を生じさせるために，それより大きい素数を見つけてきましょう．

この条件において

と下線を引いたところに注意しておいてください．

一般的に素数$M$に対して$M!+1$が素数とは限りません．

$M$が最大の素数であれば$M!+1$が素数と言っています．

まとめ